Chapter: Introduction to the Design and Analysis of Algorithms : Coping with the Limitations of Algorithm Power
Algorithms for Solving Nonlinear Equations
Algorithms for Solving Nonlinear Equations
In this section, we discuss
several algorithms for solving nonlinear equations in one unknown,

There are several reasons for
this choice among subareas of numerical analysis. First of all, this is an
extremely important problem from both a practical and the-oretical point of
view. It arises as a mathematical model of numerous phenomena in the sciences
and engineering, both directly and indirectly. (Recall, for example, that the
standard calculus technique for finding extremum points of a function f (x) is based on finding its critical points, which
are the roots of the equation f
(x) = 0.) Second, it represents the most accessible
topic in numerical analysis and, at the same time,
exhibits its typical tools and concerns. Third, some meth-ods for solving
equations closely parallel algorithms for array searching and hence provide
examples of applying general algorithm design techniques to problems of
continuous mathematics.
Let us start with dispelling
a misconception you might have about solving equations. Your experience with
equation solving from middle school to calculus courses might have led you to
believe that we can solve equations by “factoring” or by applying a readily
available formula. Sorry to break it to you, but you have been deceived (with
the best of educational intentions, of course): you were able to solve all
those equations only because they had been carefully selected to make it
possible. In general, we cannot solve equations exactly and need approximation
algorithms to do so.
This is true even for solving
the quadratic equation
ax2 + bx + c = 0
because the standard formula
for its roots

requires computing the square
root, which can be done only approximately for most positive numbers. In
addition, as we discussed in Section 11.4, this canonical formula needs to be
modified to avoid the possibility of low-accuracy solutions.
What about formulas for roots
of polynomials of degrees higher than two? Such formulas for third- and
fourth-degree polynomials exist, but they are too cumbersome to be of practical
value. For polynomials of degrees higher than four, there can be no general
formula for their roots that would involve only the polynomial’s coefficients,
arithmetical operations, and radicals (taking roots). This remarkable result
was published first by the Italian mathematician and physician Paolo Ruffini
(1765–1822) in 1799 and rediscovered a quarter century later by the Norwegian
mathematician Niels Abel (1802–1829); it was developed further by the French
mathematician Evariste Galois (1811–1832).4
The impossibility of such a
formula can hardly be considered a great disap-pointment. As the great German
mathematician Carl Friedrich Gauss (1777–1855) put it in his thesis of 1801,
the algebraic solution of an equation was no better than devising a symbol for
the root of the equation and then saying that the equation had a root equal to
the symbol [OCo98].
We can interpret solutions to
equation (12.4) as points at which the graph of the function f (x) intersects with the x-axis. The three algorithms we discuss in this
section take advantage of this interpretation. Of course, the graph of f (x) may intersect the x-axis at a single point (e.g., x3 = 0), at multiple or even infinitely many points
(sin x = 0), or at no point (e x + 1 = 0). Equation (12.4) would then
have a single root, several roots, and no roots, respectively. It is a good
idea to sketch a graph of the function before starting to approximate its
roots. It can help to determine the number of roots and their approximate
locations. In general, it is a good idea to isolate roots, i.e., to identify
intervals containing a single root of the equation in question.
Bisection
Method
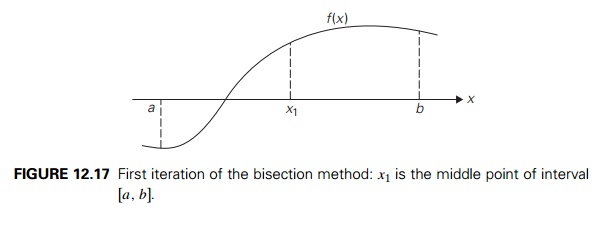
This algorithm is based on an
observation that the graph of a continuous function must intersect with the x-axis between two points a and b at least once if the function’s values have
opposite signs at these two points (Figure 12.17).
The validity of this
observation is proved as a theorem in calculus courses, and we take it for
granted here. It serves as the basis of the following algorithm, called the bisection
method, for solving equation (12.4). Starting with an interval [a, b] at whose endpoints f (x) has opposite signs, the algorithm computes the
value of
f (x) at the middle point xmid = (a + b)/2. If f
(xmid ) = 0, a root was found and the algorithm stops. Otherwise, it continues the
search for a root either on [a,
xmid ] or
on [xmid ,
b], depending on which of the two halves the values of f (x) have opposite signs at the endpoints of the
new interval.
Since we cannot expect the
bisection algorithm to stumble on the exact value of the equation’s root and
stop, we need a different criterion for stopping the algo-
rithm.
We can stop the algorithm after the interval [an, bn] bracketing some root x∗ becomes so small that we can guarantee that
the absolute error of approximating x∗ by xn, the middle point of this interval, is smaller
than some small preselected number ε > 0. Since xn is the middle point of [an, bn] and x∗ lies within this interval as well, we have

This inequality implies that
the sequence of approximations {xn} can be made as close to root x∗ as we wish by choosing n large enough. In other words, we can say that {xn} converges to root x∗. Note, however, that because any digital
computer represents extremely small values by zero (Section 11.4), the
convergence asser-tion is true in theory but not necessarily in practice. In
fact, if we choose ε below a certain
machine-dependent threshold, the algorithm may never stop! Another source of
potential complications is round-off errors in computing values of the function
in question. Therefore, it is a good practice to include in a program
im-plementing the bisection method a limit on the number of iterations the
algorithm is allowed to run.
Here is pseudocode of the
bisection method.
ALGORITHM Bisection(f (x), a, b, eps, N )
//Implements the bisection
method for finding a root of f
(x) = 0 //Input: Two real numbers a and b, a < b,
a continuous function f
(x) on [a,
b], f (a)f (b) < 0,
an upper bound on the absolute error eps > 0,
an upper bound on the number
of iterations N
//Output: An approximate (or
exact) value x of a root in (a, b)
//or an interval bracketing
the root if the iteration number limit is reached n ← 1 //iteration count
while n ≤ N do
x ← (a + b)/2
if x − a
< eps return x fval ← f
(x)
if fval = 0 return x if fval ∗f
(a) < 0
b ← x else a ← x n ← n + 1
return “iteration limit”, a, b
Note that we can use
inequality (12.7) to find in advance the number of iterations that should
suffice, at least in theory, to achieve a preselected accuracy level. Indeed,
choosing the number of iterations n large enough to satisfy (b1 − a1)/2n < ε, i.e.,
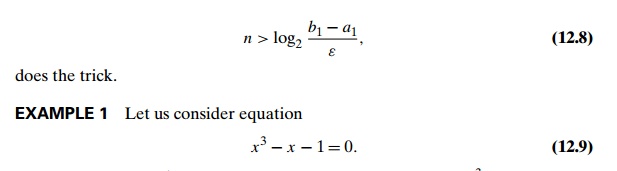
It has one real root. (See
Figure 12.18 for the graph of f
(x) = x3 − x − 1.) Since f (0)
< 0 and f
(2) > 0, the root must lie within interval [0, 2]. If we choose the error tolerance level as ε = 10−2, inequality (12.8) would require n > log2(2/10−2) or n ≥ 8 iterations.
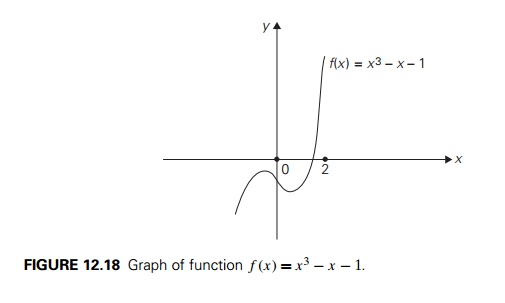
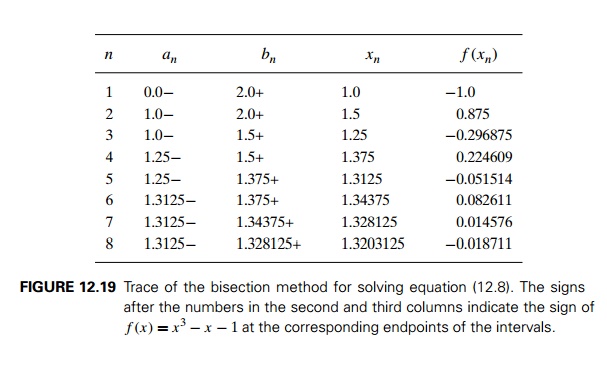
Figure 12.19 contains a trace
of the first eight iterations of the bisection method applied to equation
(12.9).
Thus, we obtained x8 = 1.3203125 as an approximate
value for the root x∗ of equation (12.9), and we can guarantee that
|1.3203125 − x∗| < 10−2.
Moreover, if we take into
account the signs of the function f
(x) at a8, b8, and x8, we can assert that the root lies between
1.3203125 and 1.328125.
The principal weakness of the
bisection method as a general algorithm for solving equations is its slow rate
of convergence compared with other known methods. It is for this reason that
the method is rarely used. Also, it cannot be extended to solving more general
equations and systems of equations. But it does have several strong points. It
always converges to a root whenever we start with an
interval whose properties are
very easy to check. And it does not use derivatives of the function f (x) as some faster methods do.
What important algorithm does
the method of bisection remind you of? If you have found it to closely resemble
binary search, you are correct. Both of them solve variations of the searching
problem, and they are both divide-by-half algorithms. The principal difference
lies in the problem’s domain: discrete for binary search and continuous for the
bisection method. Also note that while binary search requires its input array
to be sorted, the bisection method does not require its function to be
nondecreasing or nonincreasing. Finally, whereas binary search is very fast,
the bisection method is relatively slow.
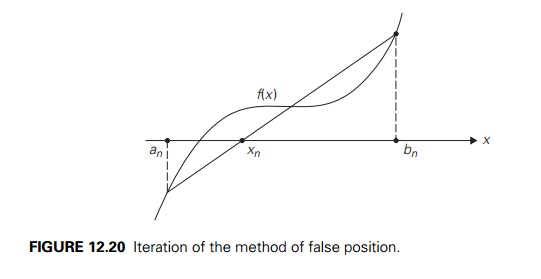
Method
of False Position
The method of false position
(also known by its name in Latin, regula falsi) is to interpolation
search as the bisection method is to binary search. Like the bisection method,
it has, on each iteration, some interval [an, bn] bracketing a root of a continuous function f (x) that has opposite-sign values at an and bn. Unlike the bisection method, however, it
computes the next root approximation not as the middle of [an, bn] but as the x-intercept of the straight line through the
points (an, f (an)) and
(bn, f (bn)) (Figure 12.20).
You are asked in the
exercises to show that the formula for this x-intercept can be written as
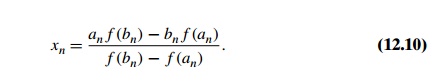
EXAMPLE
2 Figure 12.21 contains the results of the first eight iterations of
this method for solving equation (12.9).
Although for this example the
method of false position does not perform as well as the bisection method, for
many instances it yields a faster converging sequence.
Newton’s method, also called the
Newton-Raphson method, is one of the most im-portant general algorithms
for solving equations. When applied to equation (12.4) in one unknown, it can
be illustrated by Figure 12.22: the next element xn+1 of the method’s approximation sequence is
obtained as the x-intercept of the tangent
line to the graph of function f
(x) at xn.
The analytical formula for
the elements of the approximation sequence turns out to be
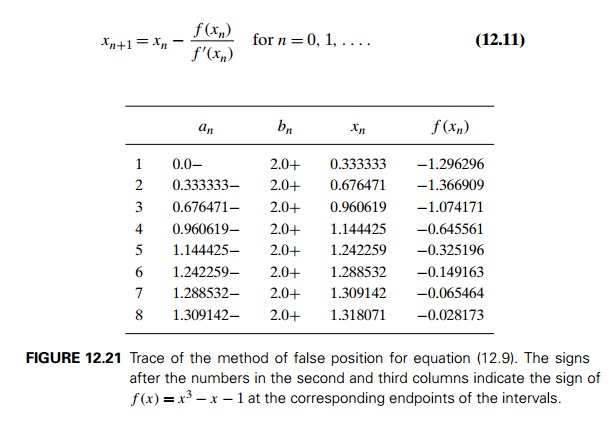
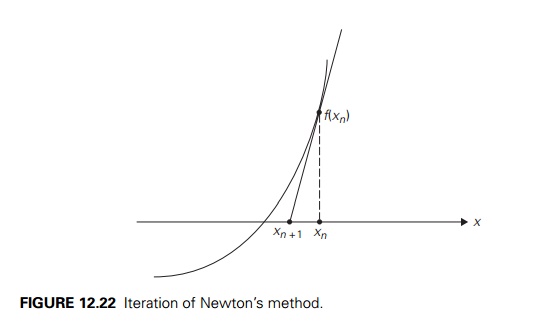
In most cases, Newton’s
algorithm guarantees convergence of sequence (12.11) if an initial approximation
x0 is chosen “close enough” to
the root. (Precisely defined prescriptions for choosing x0 can be found in numerical analysis textbooks.)
It may converge for initial approximations far from the root as well, but this
is not always true.
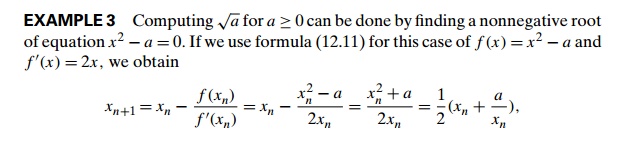
which is exactly the formula
we used in Section 11.4 for computing approximate values of square roots.
EXAMPLE
4 Let us apply Newton’s method to equation (12.9), which we
previ-ously solved with the bisection method and the method of false position.
Formula (12.11) for this case becomes
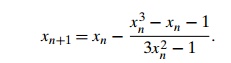
As an initial element of the
approximation sequence, we take, say, x0 = 2. Fig-ure 12.23 contains the
results of the first five iterations of Newton’s method.
You cannot fail to notice how
much faster Newton’s approximation sequence converges to the root than the
approximation sequences of both the bisection method and the method of false
position. This very fast convergence is typical of Newton’s method if an
initial approximation is close to the equation’s root. Note, however, that on
each iteration of this method we need to evaluate new values of the function
and its derivative, whereas the previous two methods require only one new value
of the function itself. Also, Newton’s method does not bracket a root as these
two methods do. Moreover, for an arbitrary function and arbitrarily chosen
initial approximation, its approximation sequence may diverge. And, because
formula (12.11) has the function’s derivative in the denominator, the method
may break down if it is equal to zero. In fact, Newton’s method is most
effective when f
(x) is bounded away from zero near root x∗. In particular, if
|f (x)| ≥ m1 > 0
on the interval between xn and x∗, we can estimate the distance between xn and x∗ by using the Mean Value Theorem of calculus as
follows:
f (xn) − f (x∗) = f (c)(xn − x∗),
where c is some point between xn and x∗. Since f (x∗) = 0 and |f (c)| ≥ m1, we obtain

Formula (12.12) can be used
as a criterion for stopping Newton’s algorithm when its right-hand side becomes
smaller than a preselected accuracy level ε. Other possible stopping criteria are
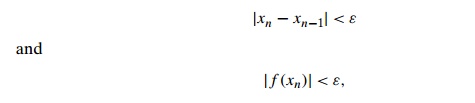
where ε is a small positive number. Since the last two
criteria do not necessarily imply closeness of xn to root x∗, they should be considered inferior to the one
based on (12.12).
The shortcomings of Newton’s
method should not overshadow its principal strengths: fast convergence for an
appropriately chosen initial approximation and applicability to much more
general types of equations and systems of equations.
Exercises 12.4
a. Find on the Internet or in
your library a procedure for finding a real root of the general cubic equation ax3 + bx2 + cx + d = 0 with real coefficients.
b. What general algorithm design technique is it based on?
Indicate how many roots each of the following equations has:
a. xex − 1 = 0 b. x − ln x = 0 c. x sin x − 1 = 0
a. Prove that if p(x) is a polynomial of an odd degree,
then it must have at least one real
root.
Prove that if x0 is a root of an n-degree polynomial p(x), the polynomial can be factored into
p(x) = (x − x0)q(x),
where q(x) is a polynomial of degree n − 1. Explain what significance
this theorem has for finding the roots of a polynomial.
c. Prove that if x0 is a root of an n-degree polynomial p(x), then
p (x0) = q(x0),
where q(x) is the quotient of the division of p(x) by x − x0.
Prove inequality (12.7).
Apply the bisection method to find the root of the equation
x3 + x − 1 = 0
with an absolute error
smaller than 10−2.
Derive formula (12.10) underlying the method of false position.
Apply the method of false position to find the root of the equation
x3 + x − 1 = 0
with an absolute error
smaller than 10−2.
Derive formula (12.11) underlying Newton’s method.
Apply Newton’s method to find the root of the equation
x3 + x − 1 = 0
with an absolute error
smaller than 10−2.
Give an example that shows that the approximation sequence of
Newton’s method may diverge.
Gobbling goat There is a grassy field in
the shape of a circle with a radius of 100
feet. A goat is attached by a rope to a hook at a fixed point on the field’s
border. How long should the rope be to let the goat reach only half of the
grass in the field?
SUMMARY
Backtracking and branch-and-bound are
two algorithm design techniques for solving
problems in which the number of choices grows at least exponentially with their
instance size. Both techniques construct a solution one component at a time,
trying to terminate the process as soon as one can ascertain that no solution
can be obtained as a result of the choices already made. This approach makes it
possible to solve many large instances of NP-hard
problems in an acceptable amount of time.
Both backtracking and
branch-and-bound employ, as their principal mech-anism, a state-space tree—a rooted tree whose nodes represent partially
constructed solutions to the problem in question. Both techniques terminate a
node as soon as it can be guaranteed that no solution to the problem can be
obtained by considering choices that correspond to the node’s descendants.
Backtracking constructs its state-space tree in the depth-first-search fashion in the majority of its applications. If
the sequence of choices represented by a current node of the state-space tree
can be developed further without violating the problem’s constraints, it is
done by considering the first remaining legitimate option for the next component.
Otherwise, the method backtracks by undoing the last component of the partially
built solution and replaces it by the next alternative.
Branch-and-bound is an algorithm design technique that enhances
the idea of generating a state-space
tree with the idea of estimating the best value obtainable from a current node
of the decision tree: if such an estimate is not superior to the best solution
seen up to that point in the processing, the node is eliminated from further
consideration.
Approximation algorithms are
often used to find approximate solutions to difficult problems of combinatorial
optimization. The performance ratio
is the principal metric for measuring the accuracy of such approximation
algorithms.
The nearest-neighbor and multifragment
heuristic are two simple greedy algorithms for approximating a solution to
the traveling salesman problem. The performance ratios of these algorithms are
unbounded above, even for the important subset of Euclidean graphs.
The twice-around-the-tree and Christofides
algorithms exploit the graph’s minimum spanning tree to construct an Eulerian
circuit and then transform it into a Hamiltonian circuit (an approximate
solution to the TSP) by shortcuts. For Euclidean graphs, the performance ratios
of these algorithms are 2 and 1.5, respectively.
Local search heuristics—the
2-opt, 3-opt, and Lin-Kernighan algorithms— work by replacing a few edges in the
current tour to find a shorter one until no such replacement can be found.
These algorithms are capable of finding in seconds a tour that is within a few
percent of optimum for large Euclidean instances of the traveling salesman
problem.
A sensible greedy algorithm
for the knapsack problem is based on processing an input’s items in descending
order of their value-to-weight ratios. For the continuous version of the
problem, this algorithm always yields an exact optimal solution.
Polynomial approximation schemes for the knapsack problem are polynomial-time
parametric algorithms that approximate solutions with any predefined accuracy
level.
Solving nonlinear equations
is one of the most important areas of numerical analysis. Although there are no
formulas for roots of nonlinear equations (with a few exceptions), several
algorithms can solve them approximately.
The bisection method and the method
of false position are continuous analogues of binary search and
interpolation search, respectively. Their principal advantage lies in
bracketing a root on each iteration of the algorithm.
Related Topics