Probability - Algebra of Events | 10th Mathematics : UNIT 8 : Statistics And Probability
Chapter: 10th Mathematics : UNIT 8 : Statistics And Probability
Algebra of Events
Algebra
of Events
In a random experiment,
let S be the sample space. Let A ⊆ S and B ⊆
S be the events in S. We say that
(i) (A Ո B) is an event that occurs only when both A
and B occurs.
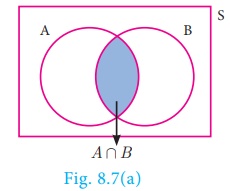
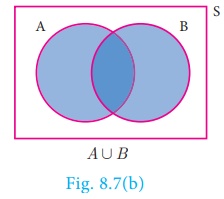
(ii) (A U B) is an event
that occurs when either one of A or B occurs.
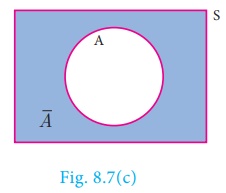
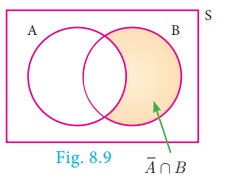
(iii) ![]() is
an event that occurs only when A doesn’t occur.
is
an event that occurs only when A doesn’t occur.
Note:
·
A ∩ ![]() = ɸ
= ɸ
·
A∪ ![]() = S
= S
·
If A, B are mutually exclusive events,
then P (A ∪ B) = P(A) + P (B)
·
P (Union of mutually exclusive events)
= ∑( Probability of events)
Thorem
1
If A and B
are two events associated with a random experiment, then prove that
(i)
P (A
Ո ![]() ) = P (only A) = P (A) −P
(A ∩ B)
) = P (only A) = P (A) −P
(A ∩ B)
(ii)
P (![]() Ո B) = P(only B) = P (B ) −P (A
∩ B)
Ո B) = P(only B) = P (B ) −P (A
∩ B)
Proof
(i) By Distributive
property of sets,
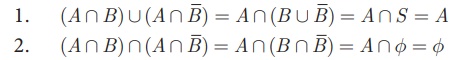
Therefore, the events A
Ո B and A Ո ![]() are mutually exclusive whose union is A.
are mutually exclusive whose union is A.
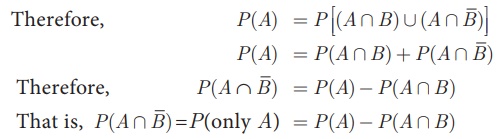

(ii) By Distributive
property of sets,
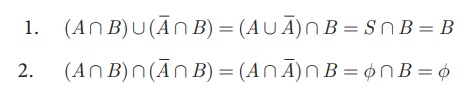
Therefore, the events A
Ո B and ![]() Ո B are mutually exclusive whose union is B.
Ո B are mutually exclusive whose union is B.
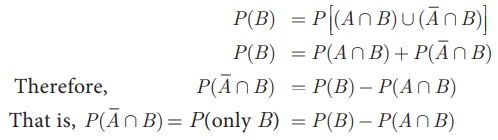
Related Topics