A proton gradient serves as an energy-rich intermediate state during ATP synthesis

A proton gradient serves as an energy-rich intermediate state during ATP synthesis

Let us first ask: How much energy is actually required in order to synthesize ATP?

The free energy for the synthesis of ATP from ADP and phosphate is calculated from the van’t Hoff equation:

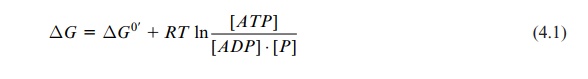
The standard free energy for the synthesis of ATP is:

                     ΔG0’  = +30.5 kJ/mol                                         (4.2)

The concentrations of ATP, ADP, and phosphate in the chloroplast stroma are very much dependent on metabolism. Typical concentrations are:

ATP = 2.5 ⋅ 10 -3 mol/L; ADP                        = 0.5 ⋅ 10 -3 mol/L; P = 5 ⋅ 10 -3 mol/L

When these values are introduced into equation 4.1 (R 8.32 J/mol · K,T 298 K), the energy required for synthesis of ATP is evaluated as:

ΔG = +47.8 kJ/mol                                                                                                            (4.3)

This value is, of course, variable because it depends on the metabolic conditions. For further considerations an average value of 50 kJ/mol will be employed for ΔGATP.

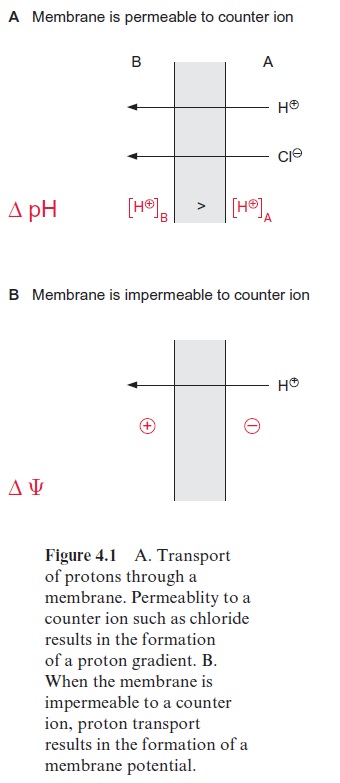
The transport of protons across a membrane can have different effects. If the membrane is permeable to counter ions of the proton (e.g., a chloride ion (Fig. 4.1A)), the charge of the proton will be compensated, since each transported proton will pull a chloride ion across a membrane. This is how a proton concentration gradient can be generated. The free energy for the transport of protons from A to B is:

                ΔG = RT ln [H+]B / [H+]A  [J/mol]

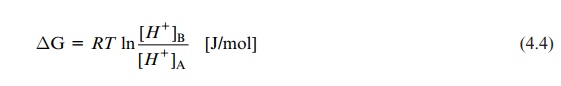
If the membrane is impermeable for counter ions (Fig. 4.1B), a charge compensation for the transported proton is not possible. In this case, the transfer of only a few protons across the membrane results in the formation of a membrane potential ΔΨ, measured as the voltage difference across the membrane. By convention,  ΔΨ is positive when a cation is transferred in the direction of the more positive region. Voltage and free energy are con-nected by the following equation:

ΔG = mF . ΔΨ                                                                                                                (4.5)

where m is the charge of the ion (in the case of a proton 1), and F is the Faraday constant, 96,485 A s/mol.

Proton transport across a biological membrane leads to the formation of a proton concentration gradient and a membrane potential. The free energy for the transport of protons from A to B therefore consists of the sum of the free energies for the generation of the H+concentration gradi-ent and the membrane potential:

ΔG = RT ln•[H+]B  / [H+]A + FΔΨ

In chloroplasts, the energy stored in a proton gradient corresponds to the change of free energy during the flux of protons from the lumen into the stroma.

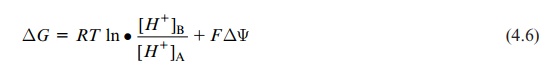
ΔG = RT ln [H+]S / [H+]L + FΔΨ

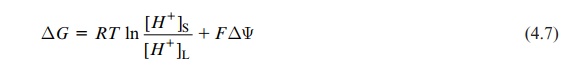
where S = stroma, L=lumen, and ΔΨ=voltage difference stroma-lumen. The conversion of the natural logarithm into the decadic logarithm yields:

    ΔG = 2.3 . RT log [H+]S / [H+]L + FΔΨ

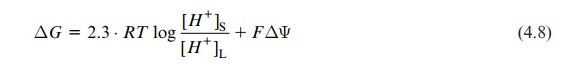
The logarithmic factor is the negative pH difference between lumen and stroma:

Log[H+]S –log[H+]L = -ΔpH

A rearrangement yields:

ΔG = -2.3RT •  ΔpH + FΔΨ                                                                                 (4.10)

At 25°C:                                                         2.3 . RT = 5,700 J /mol

Thus:                                                                              ΔG = -5,700  ΔpH + FΔΨ       [J/mol]                                                                             (4.11)

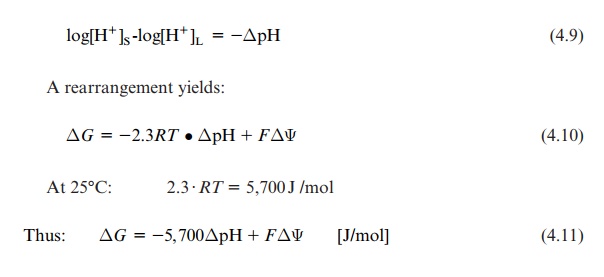
The expression ΔG / F is called proton motive force (PMF) (unit in volts):

ΔG / F = PMF = - 2.3RT / F . ΔpH + ΔΨ   [V]

AT 250C:         2.3RT / F = 0.059V

Thus:                                                              PMF = -0.059 ⋅  ΔpH + ΔΨ   [V]                (4.13)

Equation 4.13 is of general significance for electron transport-coupled ATP synthesis. In mitochondrial oxidative phosphorylation, the PMF is primarily the result of a membrane potential. In chloroplasts, on the other hand, the membrane potential does not contribute much to the PMF, since the PMF is almost entirely due to the concentration gradient of protons across the thylakoid membrane. Inilluminated chloroplasts, a ΔpH across the thylakoid membrane of about 2.5 can be measured. Introducing this value into equation 4.11 yields:

                            ΔG = -14.3 kJ/mol

A comparison of this value with ΔG for the formation of ATP (50 kJ/ mol) suggests that at least four protons are required for the ATP synthesis from ADP and phosphate.