Set Covering Problem- Integer Linear Programming Illustrative Applications

Set-Covering Problem

In this class of problems, overlapping services are offered by a number of installations to a number of facilities. The objective is to determine the minimum number of installations that will cover (i.e., satisfy the service needs) of each facility. For example, water treatment plants can be constructed at various locations, with each plant serving different sets of cities. The overlapping arises when a given city can receive service from more than one plant.

Example 9.1-2  (Installing Security Telephones)

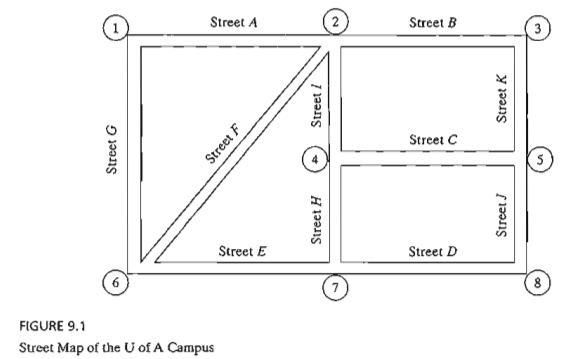
To promote on-campus safety, the U of A Security Department is in the process of installing emergency telephones at selected locations. The department wants to install the minimum number of telephones, provided that each of the campus main streets is served by at least one telephone. Figure 9.1 maps the principal streets (A to K) on campus.

It is logical to place the telephones at street intersections so that each telephone will serve at least two streets. Figure 9.1 shows that the layout of the streets requires a maximum of eight telephone locations.

Define

The constraints of the problem require installing at least one telephone on each of the 11 streets (A to K). 

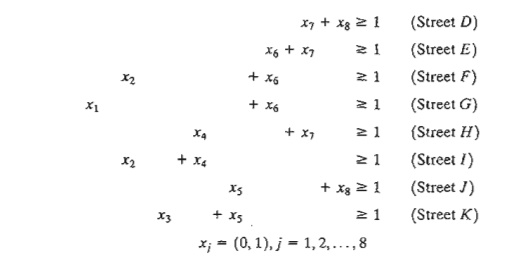
The optimum solution of the problem requires installing four telephones at intersections 1,2,5, and 7.

Remarks. In the strict sense, set-covering problems are characterized by (1) the variables X_j, j = 1,2, ... , n, are binary, (2) the left-hand-side coefficients of the constraints are 0 or 1, (3) the right-hand side of each constraint is of the form (≥ 1), and (4) the objective function minimizes c₁x₁ + c₂x₂ + ... + c_nx_m where cj > 0 for all j = 1,2, ... , n. In the present example, c_j = 1 for all j. If cj represents the installation cost in location j, then these coefficients may assume values other than 1. Variations of the set-covering problem include additional side conditions, as some of the situ-ations in Problem Set 9.lb show.

AMPlMoment

Figure 9.2 presents a general AMPL model for any set-covering problem (file am-pIEx9.1-2.txt). The formulation is straightforward, once the use of indexed set is under-stood (see Section AA). The model defines street as a (regular) set whose elements

are A through K. Next, the indexed set corner{street} defines the corners as a function of street. With these two sets, the constraints of the model can be formulated directly. The data of the model give the elements of the indexed sets that are specific to the situation in Example 9.1-2. Any other situation is handled by changing the data of the model.

PROBLEM SET 9.1 B

*1. ABC is an LTL (less-than-truckload) trucking company that delivers loads on a daily basis to five customers. The following list provides the customers associated with each route:

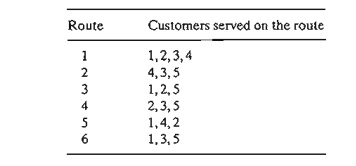
The segments of each route are dictated by the capacity of the truck delivering the loads. For example, on route 1, the capacity of the truck is sufficient to deliver the loads to customers 1,2,3, and 4 only. The following table lists distances (in miles) among the truck terminal (ABC) and the customers.

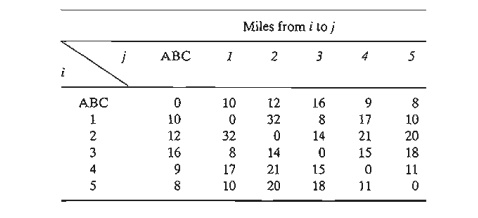
The objective is to determine the least distance needed to make the daily deliveries to all five customers. Though the solution may result in a customer being served by more than one route, the implementation phase will use only one such route. Formulate the problem as an ILP and find the optimum solution.

*2. The U of A is in the process of forming a committee to handle students' grievances. The administration wants the committee to include at least one female, one male, one student, one administrator, and one faculty member. Ten individuals (identified, for simplicity, by the letters a to j) have been nominated. The mix of these individuals in the different categories is given as follows:

The U of A wants to form the smallest committee with representation from each of the five categories. Formulate the problem as an ILP and find the optimum solution.

3. Washington County includes six towns that need emergency ambulance service. Because of the proximity of some of the towns, a single station may serve more than one commu-nity. The stipulation is that the station must be within 15 minutes of driving time from the towns it serves. The table below gives the driving times in minutes among the six towns.

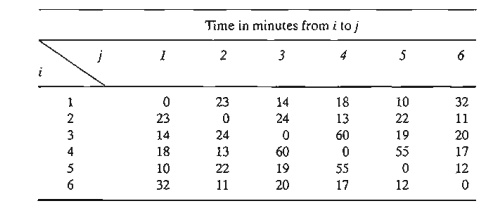
Formulate an ILP whose solution will produce the smallest number of stations and their locations. Find the optimum solution.

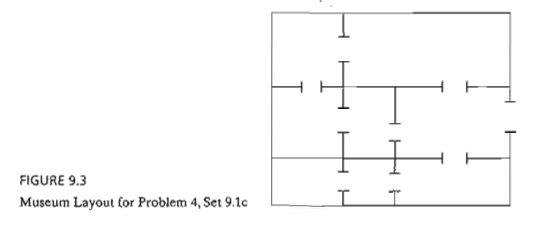
4. The treasures of King Tut are on display in a museum in New Orleans. The layout of the museum is shown in Figure 9.3, with the different rooms joined by open doors. A guard standing at a door can watch two adjoining rooms. The museum wants to ensure guard presence in every room, using the minimum number possible. Formulate the problem as an ILP and find the optimum solution.

5. Bill has just completed his exams for the academic year and wants to celebrate by seeing every movie showing in theaters in his town and in six other neighboring cities. If he trav-els to another town, he will stay there until he has seen all the movies he wants. The fol-lowing table provides the information about the movie offerings and the round-trip distance to the neighboring town.

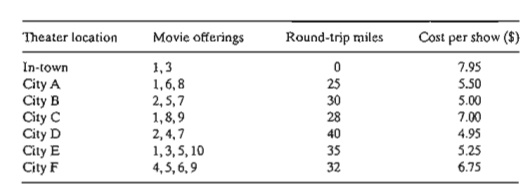
The cost of driving is 75 cents per mile. Bill wishes to determine the towns he needs to visit to see all the movies while minimizing his total cost.

6. Walmark Stores is in the process of expansion in the western United States. During the next year, Walmark is planning to construct new stores that will serve 10 geographically dispersed communities. Past experience indicates that a community must be within 25 miles of a store to attract customers. In addition, the population of a community plays an important role in where a store is located, in the sense that bigger communities generate more participating customers. The following tables provide the populations as well as the distances (in miles) between the communities:

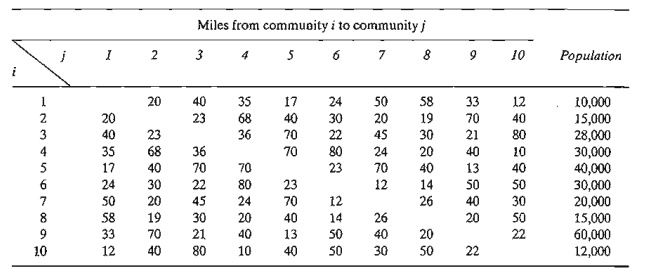
The idea is to construct the least number of stores, taking into account the distance restriction and the concentration of populations.

Specify the communities where the stores should be located.

*7. (Gueret and Associates, 2002, Section 12.6) MobileCo is budgeting 15 million dollars to construct as many as 7 transmitters to cover as much population as possible in 15 con-tiguous geographical communities. The communities covered by each transmitter and the budgeted construction costs are given below.

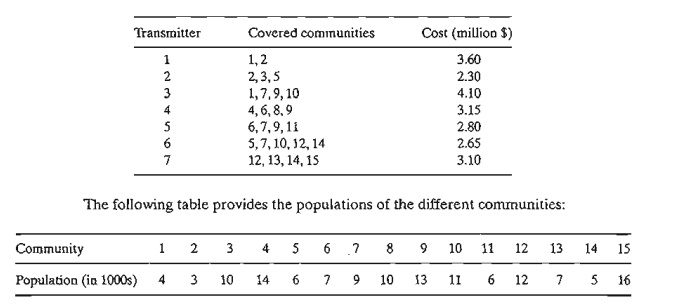
Which of the proposed transmitters should be constructed?

8. (Gavernini and Associates, 2004) In modern electric networks, automated electric utility meter reading replaces the costly labor-intensive system of manual meter reading. In the

automated system, meters from several customers are linked wirelessly to a single receiv-er. The meter sends montWy signals to a designated receiver to report the customer's consumption of electricity. The receiver then sends the data to a central computer to gen-erate the electricity bills. The problem reduces to determining the least number of re-ceivers needed to serve a number of customers. In real life, the problem encompasses thousands of meters and receivers. However, for the purpose of this problem, consider the case of 10 meters and 8 receivers, using the following configurations:

Determine the minimum number of receivers.

9. Solve Problem 8 if, additionally, each receiver can handle at most 3 meters.