Recursive Nature of Computations in DP(Dynamic Programming)

RECURSIVE NATURE OF COMPUTATIONS IN DP

Computations in DP are done recursively, so that the optimum solution of one subproblem is used as an input to the next subproblem. By the time the last subproblem is solved, the optimum solution for the entire problem is at hand. The manner in which the recursive computations are carried out depends on how we decompose the original problem. In particular, the subproblems are normally linked by common constraints. As we move from one subproblem to the next, the feasibility of these common constraints must be maintained.

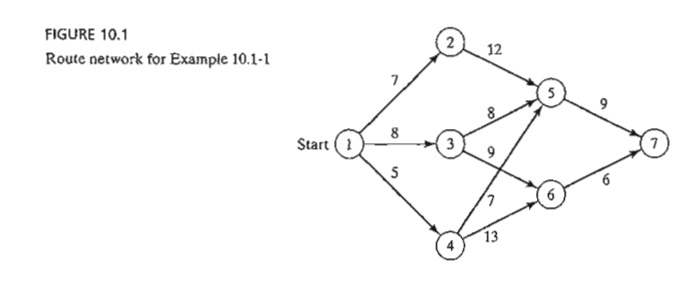
Example 10.1-1   (Shortest-Route Problem)

Suppose that you want to select the shortest highway route between two cities. The network in Figure 10.1 provides the possible routes between the starting city at node 1 and the destination city at node 7. The routes pass through intermediate cities designated by nodes 2 to 6.

We can solve this problem by exhaustively enumerating all the routes between nodes 1 and 7 (there are five such routes). However, in a large network, exhaustive enumeration may be intractable computationally. '

To solve the problem by DP, we first decompose it into stages as delineated by the vertical dashed lines in Figure 10.2. Next, we carry out the computations for each stage separately.

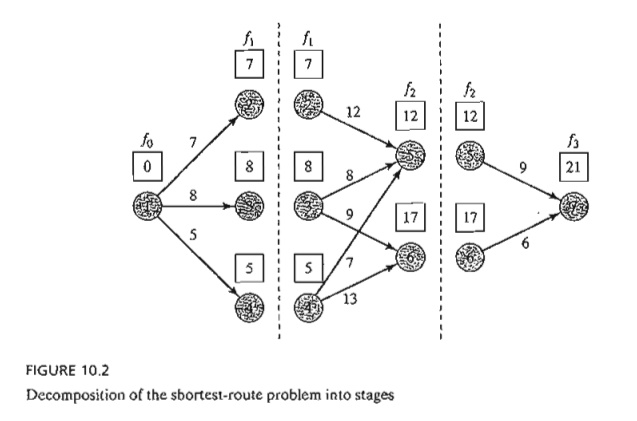
The general idea for determining the shortest route is to compute the shortest (cumulative) distances to all the terminal nodes of a stage and then use these distances as input data to the immediately succeeding stage. Starting from node 1, stage 1 includes three end nodes (2,3, and 4) and its computations are simple.

Stage 1 Summary.

Shortest distance from node 1 to node 2 = 7 miles (from node 1)

Shortest distance from node 1 to node 3 = 8 miles (from node 1)

Shortest distance from node 1 to node 4 = 5 miles (from node 1)

Next, stage 2 has two end nodes, 5 and 6. Considering node 5 first, we see from Figure 10.2 that node 5 can be reached from three nodes, 2,3, and 4, by three different routes: (2,5), (3,5), and (4, 5). This information, together with the shortest distances to nodes 2, 3, and 4, determines the shortest (cumulative) distance to node 5 as

Stage 2 Summary.

Shortest distance from node 1 to node 5 = 12 miles (from node 4)

Shortest distance from node 1 to node 6 =  17 miles (from node 3)

The last step is to consider stage 3. The destination node 7 can be reached from either nodes 5 or 6. Using the summary results from stage 2 and the distances from nodes 5 and 6 to node 7, we get

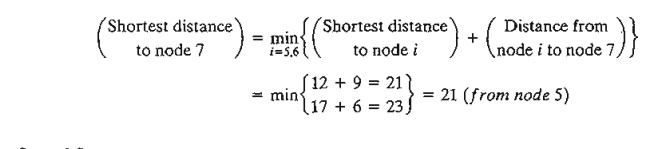
Stage 3 Summary.

Shortest distance from node 1 to node 7 = 21 miles (from node 5)

Stage 3 summary shows that the shortest distance between nodes 1 and 7 is 21 miles. To deter-mine the optimal route, stage 3 summary links node 7 to node 5, stage 2 summary links node 4 to node 5, and stage 1 summary links node 4 to node 1. Thus, the shortest route is 1 - >  4 - >  5 - >  7.

The example reveals the basic properties of computations in DP:

a)     The computations at each stage are a function of the feasible routes of that stage, and that stage alone.

b)    A current stage is linked to the immediately preceding stage only without regard to earlier stages. The linkage is in the form of the shortest-distance summary that represents the out-put of the immediately preceding stage.

Recursive Equation. We now show how the recursive computations in Example 10.1-1 can be expressed mathematically. Let f_i(x_i) be the shortest distance to node x_i at stage 4 and define d(x_i-₁, x_i) as the distance from node x_i-l to node x_i, then f_i is computed from f_i-1 using the following recursive equation:

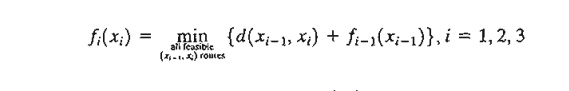
Starting at i = 1, the recursion sets f_o(x_o) = 0. The equation shows that the shortest distances f_i(x_j) at stage i must be expressed in terms of the next node, x_i. In the DP terminology, x_i is referred to as the state of the system at stage i. In effect, the state of the system at stage i is the information that links the stages together, so that optimal decisions for the remaining stages can be made without reexamining how the decisions for the previous stages are reached. The proper definition of the state allows us to consider each stage separately and guarantee that the solution is feasible for all the stages.

The definition of the state leads to the following unifying framework for DP.

Principle of Optimality

Future decisions for the remaining stages will constitute an optimal policy regardless of the policy adopted in previous stages.

The implementation of the principle is evident in the computations in Example 10.1-1. For example, in stage 3, we only use the shortest distances to nodes 5 and 6, and do not concern ourselves with how these nodes are reached from node 1. Although the principle of optimality is "vague" about the details of how each stage is optimized, its application greatly facilitates the solution of many complex problems.

PROBLEM SET 10.lA

*1. Solve Example 10.1-1, assuming the following routes are used:

2. I am an avid hiker. Last summer, I went with my friend G. Don on a 5-day hike-and-camp trip in the beautiful White Mountains in New Hampshire. We decided to limit our hiking to an area comprising three well-known peaks: Mounts Washington, Jefferson, and Adams. Mount Washington has a 6-mile base-to-peak trail. The corresponding base-ta-peak trails for Mounts Jefferson and Adams are 4 and 5 miles, respectively. The trails joining the bases of the three mountains are 3 miles between Mounts Washington and Jefferson, 2 miles between Mounts Jefferson and Adams, and 5 miles between Mounts Adams and Washington. We started on the first day at the base of Mount Washington and returned to the same spot at the end of 5 days. Our goal was to hike as many miles as we could. We also decided to climb exactly one mountain each day and to camp at the base of the moun-tain we would be climbing the next day. Additionally, we decided that the same mountain could not be visited in any two consecutive days. How did we schedule our hike?