Harmonic Analysis

Harmonic Analysis

The process of finding the Fourier series for a function given by numerical values is known as harmonic analysis.

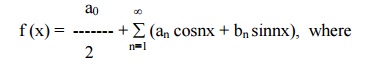
ie, f(x) = (a0/2) + (a1 cosx + b1 sinx) + (a2 cos2x + b2 sin2x) + (a3cos3x + b3sin3x)+-------------…(1)

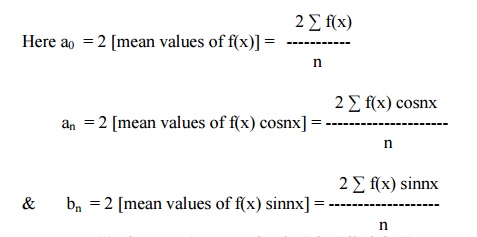
In (1), the term (a1cosx + b1 sinx) is called the fundamental or first harmonic, the term (a2cos2x + b2sin2x) is called the second harmonic and so on.

Example 16

Compute the first three harmonics of the Fourier series of f(x) given by the following table.

We    exclude   the   last   point   x   =   2Ï€.

Let  f(x) = (a0/2) + (a1 cosx + b1 sinx) + (a2 cos2x + b2 sin2x) + …………

To evaluate the coefficients, we form the following table.

\ f(x) = 1.45 – 0.37cosx + 0.17 sinx – 0.1cos2x – 0.06 sin2x + 0.033 cos3x+…

Example 17

Obtain the first three coefficients in the Fourier cosine series for y, where y is given in the following table:

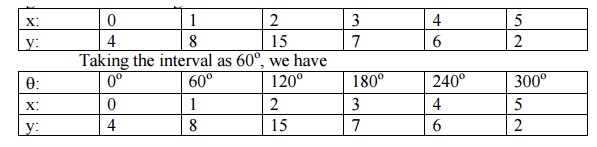
\ Fourier cosine series in the interval (0, 2Ï€) is y = (a0 /2) + a1cosq+ a2cos2q+ a3cos3q+ …..

To evaluate the coefficients, we form the following table.

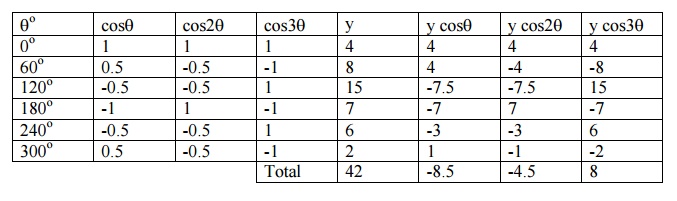
Now,         a0 = 2 (42/6) = 14

a1 = 2 ( -8.5/6) = - 2.8

a2 = 2        (-4.5/6) =

a3 = 2 (8/6) = 2.7

y = 7 –2.8 cosq- 1.5 cos2q+ 2.7 cos3q+   â€¦..

Example 18

The values of x and the corresponding values of f(x) over a period T are given below. Show that  f(x) = 0.75 + 0.37 cosq+ 1.004 sinq,where q= (2Ï€x   )/T

We omit the last value since f(x) at x = 0 is known. 

Here q= 2Ï€x / T

When x varies from 0 to T, qvaries from   0   to   2Ï€   with2Ï€/6.   an   incre

Let  f(x) = F(q) = (a0/2) + a1 cosq+ b1 sinq.

To evaluate the coefficients, we form the following table.

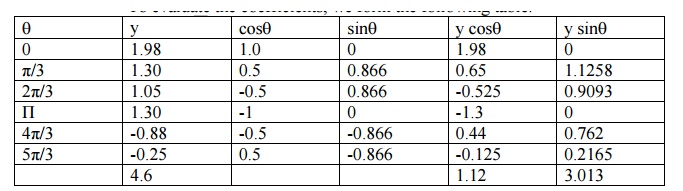
Now, a0  = 2 ( ∑   f(x)/6)=1.5

a1 = 2 (1.12 /6) = 0.37

a2 = 2 (3.013/6) =  1.004

Therefore, f(x) = 0.75 + 0.37 cosq+ 1.004 sinq

Exercises

1.The following table gives the variations of periodic current over a period.

t (seconds)   :        0        T/6    T/3    T/2    2T/3  5T/6  T

A (amplitude): 1.98       1.30   1.05   1.30   -0.88 -0.25 1.98

Show that there is a direct current part of 0.75 amp in the variable current and obtain the

amplitude of the first harmonic.                                    

2.The turning moment  T is given for a series of values of the crank angle q°=75°

q°      :         0        30      60      90      120    150    180

T°      :         0        5224  8097  7850  5499  2626  0

Obtain the first four terms in a series of sines to represent T and calculate

T for q= 75°

3. Obtain the constant term and the co-efficient of the first sine and cosine terms in the

Fourier   expansionfollowingof table„y‟.   as   given   in   th

X       :         0        1        2        3        4        5        

Y       :         9        18      24      28      26      20      

4. Find the first three harmonics of Fourier series of y = f(x) from the following data. 

X : 0 Â° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330°

Y : 298  356373  337     254    15580         516093       147    221    

2.8 Complex Form of Fourier Series                                       

The series for f(x) defined in the        interval (c, c+2Ï€)and satisfying