Flat Plate Collector Efficiency Factor

Collector Efficiency Factor

 The heat lost from the collector can thus be calculated, if the average plate temperature is known. However, this temperature is generally not known. It will, therefore be necessary to consider the flow of heat in the absorber plate and across the fluid tubes to the fluid so that the values of T_pm can be related to the value of the inlet fluid temperature which is a known quantity.

In order to simplify the problem, the approach adopted will be to conduct the a number of one- dimensional analysis. First, the one – dimensional low of heat in the absorber plate in a direction at right angles to the direction of fluid flow will be considered. This will be followed by a consideration of the heat flow from the plate to the fluid across the tube wall. Finally, the one – dimensional flow of fluid inside the tube will be analyzed.

Consider a collector having an absorber plate of length L₁ and width L₂. Assume that there are N fluid tubes and that the pitch of the tube is W = (L₂/N). Let D_i and D_o be the inside and outside diameter of the tubes.

Consider a section of the absorber plate with two adjacent fluid tubes. The temperature in the plate(T_p) will vary in the x-direction in the manner as shown in Fig 4.27. It will be assumed that the same distribution exists between any two tubes. Above the fluid tubes, the temperature will be constant, while in between the tubes, temperature will pass through the maximum. Taking a slice ‘dy’ along the flow direction and neglecting heat conduction in the plate in that direction, we can write energy balance for an element dx x dy of the plate.

(Net heat conducted into element) + (Incident energy absorbed) = ( Heat lost from Element)

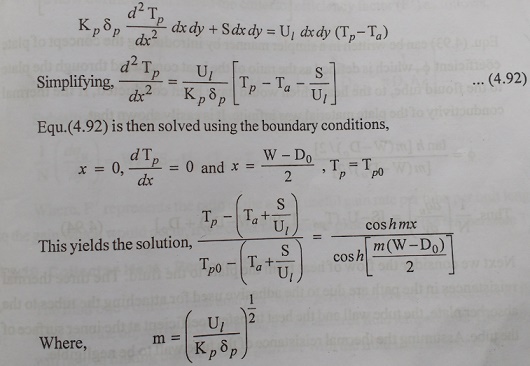
The temperature distribution obtained is similar to that for a long rectangular fin. The rate at which energy is conducted through the plate to one fluid tube from both sides.

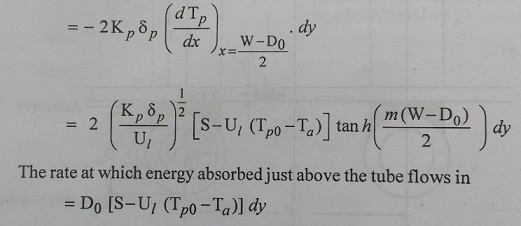
Equ.(4.93) can be written in a simpler manner by introducing the concept of plate coefficient Ï•, which is defined as the heat conducted through the plate to the flouid tube, to the heat which would have been conducted, I the thermal conductivity of the plate material was infinite. It is easily shown that,

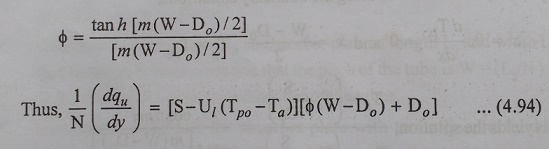
Next we consider the flow of heat from the plate to the fluid. The three thermal resistances in the path are due to the adhesive used for attaching the tubes to the absorber plate, the tube wall and the heat transfer coefficient at the inner surface of the tube. Assuming the thermal resistance of the tube wall to be negligible.

Where, F‘ represents the ratio of the actual useful gain rate per tube per unit length to the gain which would occur, if the collector absorber plate where at the temperature T_f.