Chapter: Mechanical : Strength of Materials : Deflection of Beams
Evaluation of beam deflection and slope
Evaluation of beam deflection and slope
Beam deflection
Static beam equation

Bending of an Euler-Bernoulli beam. Each cross-section of the beam is at 90 degrees to the neutral axis.
The Euler-Bernoulli equation describes the relationship between the beam's deflection and the applied load
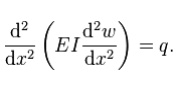
The curve w(x) describes the deflection w of the beam at some position x (recall that the beam is modeled as a one-dimensional object). q is a distributed load, in other words a force per unit length (analogous to pressure being a force per area); it may be a function of x, w, or other variables.
Note that E is the elastic modulus and that I is the second moment of area. I must be calculated with respect to the centroidal axis perpendicular to the applied loading. For an Euler-Bernoulli beam not under any axial loading this axis is called the neutral axis.
Often, w = w(x), q = q(x), and EI is a constant, so that:
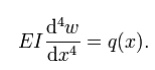
This equation, describing the deflection of a uniform, static beam, is used widely in engineering practice. Tabulated expressions for the deflection wfor common beam configurations can be found in engineering handbooks. For more complicated situations the deflection can be determined by solving the Euler-Bernoulli equation using techniques such as the "slope deflection method", "moment distribution method", "moment area method, "conjugate beam method", "the principle of virtual work", "direct integration", "Castigliano's method", "Macaulay's method" or the "direct stiffness method".
Successive derivatives of w have important meanings:

The stresses in a beam can be calculated from the above expressions after the deflection due to a given load has been determined.
A number of different sign conventions can be found in the literature on the bending of beams and care should be taken to maintain consistency. In this article, the sign convention has been chosen so the coordinate system is right handed. Forces acting in the positive x and z directions are assumed positive. The sign of the bending moment is chosen so that a positive value leads to a tensile stress at the bottom cords. The sign of the shear force has been chosen such that it matches the sign of the bending moment.
Double integration method
The double integration method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.
Thus, EI / M = 1 / y''
.
Macaulay Method
The starting point for Maucaulay's method is the relation between bending moment and curvature from Euler-Bernoulli beam theory
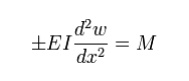
This equation is simpler than the fourth-order beam equation and can be integrated twice to find w if the value of M as a function of x is known. For general loadings, M can be expressed in the form
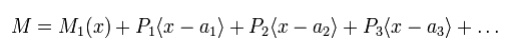
where the quantities Pi(x-ai) represent the bending moments due to point loads and the quantity (x-ai) is a Macaulay bracket defined as

Ordinarily, when integrating P(x - a) we get
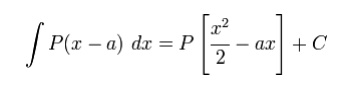
However, when integrating expressions containing Macaulay brackets, we have
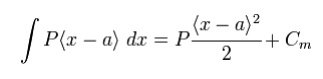
with the difference between the two expressions being contained in the constant Cm. Using these integration rules makes the calculation of the deflection of Euler-Bernoulli beams simple in situations where there are multiple point loads and point moments. The Macaulay method predates more sophisticated concepts such as Dirac delta functions and step functions but achieves the same outcomes for beam problems.
Example: Simply supported beam with point load
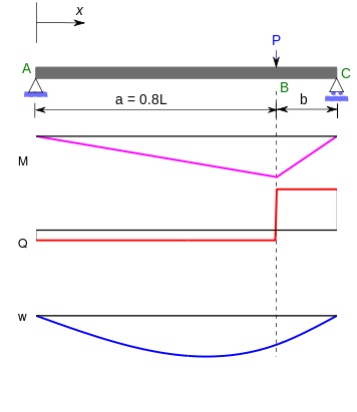
Simply supported beam with a single eccentric concentrated load.
An illustration of the Macaulay method considers a simply supported beam with a single eccentric concentrated load as shown in the adjacent figure. The first step is to find M. The reactions at the supports A and C are determined from the balance of forces and moments as
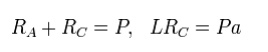
Therefore RA = Pb / L and the bending moment at a point D between A and B (0 < x < a) is given by
M = RAx = Pbx / L
Using the moment-curvature relation and the Euler-Bernoulli expression for the bending moment, we have

For a point D in the region BC (a < x < L), the bending moment is
M = RAx - P(x - a) = Pbx / L - P(x - a)
In Macaulay's approach we use the Macaulay bracket form of the above expression to represent the fact that a point load has been applied at location B, i.e.,
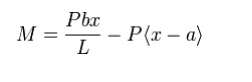
Therefore the Euler-Bernoulli beam equation for this region has the form
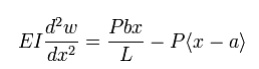

Comparing equations (iii) & (vii) and (iv) & (viii) we notice that due to continuity at point B, C1 = D1 and C2 = D2. The above observation implies that for the two regions considered, though the equation for bending moment and hence for the curvature are different, the constants of integration got during successive integration of the equation for curvature for the two regions are the same.
The above argument holds true for any number/type of discontinuities in the equations for curvature, provided that in each case the equation retains the term for the subsequent region
in the form ( x-a)n, ( x-b)n, ( x-c)n etc. It should be remembered that for any x, giving the quantities within the brackets, as in the above case, -ve should be neglected, and the calculations should be made considering only the quantities which give +ve sign for the terms within the brackets.
Reverting back to the problem, we have
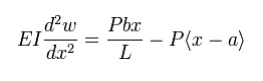
It is obvious that the first term only is to be considered for x < a and both the terms for x > a and the solution is
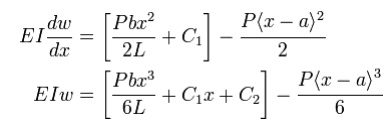
Note that the constants are placed immediately after the first term to indicate that they go with the first term when x < a and with both the terms when x > a. The Macaulay brackets help as a reminder that the quantity on the right is zero when considering points with x < a.
Related Topics