Capital Budgeting- Integer Linear Programming Illustrative Applications

ILLUSTRATIVE APPLICATIONS

This section presents a number of ILP applications. The applications generally fall into two categories: direct and transformed. In the direct category, the variables are natural-ly integer and may assume binary (0 or 1) or general discrete values. For example, the problem may involve determining whether or not a project is selected for execution (binary) or finding the optimal number of machines needed to perform a task (general discrete value). In the transfonned category, the original problem, which may not involve any integer variables, is analytically intractable. Auxiliary integer variables (usu-ally binary) are used to make it tractable. For example, in sequencing two jobs, A and B, on a single machine, job A may precede job B or job B may precede job A. The "or" nature of the constraints is what makes the problem analytically intractable, because all mathematical programming algorithms deal with "and" constraints only. The situa-tion is remedied by using auxiliary binary variables to transform the "or" constraints into equivalent "and" constraints.

For convenience, a pure integer problem is defined to have all integer variables. Otherwise, a problem is a mixed integer program if it deals with both continuous and integer variables.

1. Capital Budgeting

This section deals with decisions regarding whether or not investments should be made in individual projects. The decision is made under limited-budget considerations as well as priorities in the execution of the projects.

Example 9.1-1   (Project Selection)

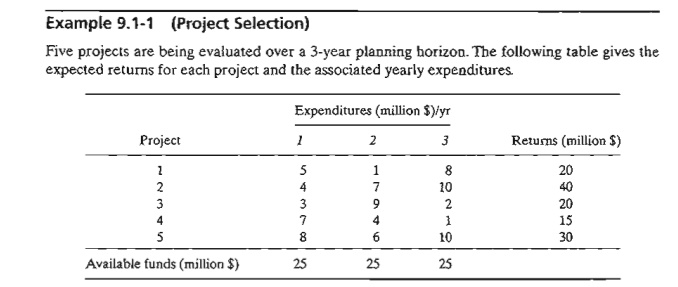
Five projects are being evaluated over a 3-year planning horizon. The following table gives the expected returns for each project and the associated yearly expenditures.

Which projects should be selected over the 3-year horizon?

The problem reduces to a "yes-no" decision for each project. Define the binary variable x_j as

The optimum integer solution (obtained by AMPL, Solver, or TORA) is x₁ =x₂ = x₃ = x₄ = 1, x₅ = 0, with z = 95 (million $). The solution shows that all but project 5 must be selected.

Remarks. It is interesting to compare the continuous LP solution with the ILP solution. The LP optimum, obtained by replacing x_j = (0,1) with 0 ≤ x_j ≤ 1 for all j, yields x₁ = .5789, x₂ = x₃ = x₄ = 1, x₅ = .7368, and z = 108.68 (million $). The solution is meaningless because two of the variables assume fractional values. We may round the solution to the closest integer values, which yields x₁ = x₅ = 1. However, the resulting solution is infeasible because the constraints are violated. More important, the concept of rounding is meaningless here because x_i rep-resents a "yes-no" decision.

PROBLEM SET 9.1A

1. Modify and solve the capital budgeting model of Example 9.1-1 to account for the fol-lowing additional restrictions:

a)      Project 5 must be selected if either project 1 or project 3 is selected.

b)      Projects 2 and 3 are mutually exclusive.

2. Five items are to be loaded in a vessel. The weight w_i, volume v_i, and value r_i for item i are tabulated below.

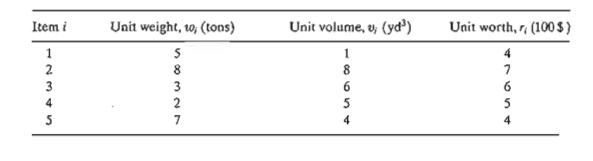
The maximum allowable cargo weight and volume are 112 tons and 109 yd³ , respectively. Formulate the ILP model, and find the most valuable cargo.

*3. Suppose that you have 7 full wine bottles, 7 half-full, and 7 empty. You would like to divide the 21 bottles among three individuals so that each will receive exactly 7. Addition-ally, each individual must receive the same quantity of wine. Express the problem as ILP constraints, and find a solution. (Hint: Use a dummy objective function in which all the objective coefficients are zeros.)

4. An eccentric sheikh left a will to distribute a herd of camels among his three children: Tarek receives at least one-half of the herd, Sharif gets at least one third, and Maisa gets at least one-ninth. The remainder goes to charity. The will does not specify the size of the herd except to say that it is an odd number of camels and that the named charity receives exactly one camel. Use ILP to determine how many camels the sheikh left in the estate and how many each child got.

5. A farm couple are sending their three children to the market to sell 90 apples with the objective of educating them about money and numbers. Karen, the oldest, carries 50 apples; Bill, the middle one, carries 30; and John, the youngest, carries only 10. The parents have stipulated five rules: (a) The selling price is either $1 for 7 apples or $3 for 1 apple, or a combination of the two prices. (b) Each child may exercise one or both options of the selling price. (c) Each of the three children must return with exactly the same amount of money. (d) Each child's income must be in whole dollars (no cents allowed). (e) The amount received by each child must be the largest possible under the stipulated condi-tions. Given that the three kids are able to sell all they have, use ILP to show how they can satisfy the parents' conditions.

*6. Once upon a time, there was a captain of a merchant ship who wanted to reward three crew members for their valiant effort in saving the ship's cargo during an unexpected storm in the high seas. The captain put aside a certain sum of money in the purser's office and instructed the first officer to distribute it equally among the three mariners after the ship had reached shore. One night, one of the sailors, unbeknown to the others, went to the purser's office and decided to claim (an equitable) one-third of the money in advance. After he had divided the money into three equal shares, an extra coin remained, which the mariner decided to keep (in addition to one-third of the money). The next night, the second mariner got the same idea and, repeating the same three-way division with what was left, ended up keeping an extra coin as well. The third night, the third mariner also took a third of what was left, plus an extra coin that could not be divided. When the ship reached shore, the first officer divided what was left of the money equally among the three mariners, again to be left with an extra coin. To simplify things, the first officer put the extra coin aside and gave the three mariners their allotted equal shares. How much money was in the safe to start with? Formulate the problem as an ILP, and find the solution. (Hint: The problem has a countably infinite number of integer solutions. For convenience, assume that we are interested in determining the smallest sum of money that satisfies the problem conditions. Then, boosting the resulting sum by 1, add it as a lower bound and obtain the next smallest sum. Continuing in this manner, a general solution pattern will evolve.)

7. (Weber, 1990) You have the following three-letter words: AFT, FAR, TVA, ADV, JOE, FIN, OSF, and KEN. Suppose that we assign numeric values to the alphabet starting with A = 1 and ending with Z = 26. Each word is scored by adding numeric codes of its three letters. For example, AFT has a score of 1 + 6 + 20 = 27. You are to select five of the given eight words that yield the maximum total score. Simultaneously, the selected five words must satisfy the following conditions:

Formulate the problem as an ILP, and find the optimum solution.

8. Solve Problem 7 given that, in addition to the total sum being the largest, the sum of col-umn 1 and the sum of column 2 will be the largest as well. Find the optimum solution.

9. (Weber, 1990) Consider the following two groups of words:

All the words in groups 1 and 2 can be formed from the nine letters A, E, F, H, 0, P, R, S, and T. Develop a model to assign a unique numeric value from 1 through 9 to these let-ters such that the difference between the total scores of the two groups will be as small as possible. [Note: The score for a word is the sum of the numeric values assigned to its individual letters.]

*10. The Record-a-Song Company has contracted with a rising star to record eight songs. The durations of the different songs are 8,3,5,5,9,6,7, and 12 minutes, respectively. Record-a-Song uses a two-sided cassette tape for the recording. Each side has a capacity of 30 minutes. The company would like to distribute the songs between the two sides such that the length of the songs on each side is about the same. Formulate the problem as an ILP, and find the optimum solution.

11. In Problem 10, suppose that the nature of the melodies dictates that songs 3 and 4 cannot be recorded on the same side. Formulate the problem as an ILP. Would it be possible to use a 25-minute tape (each side) to record the eight songs? If not, use ILP to determine the minimum tape capacity needed to make the recording.

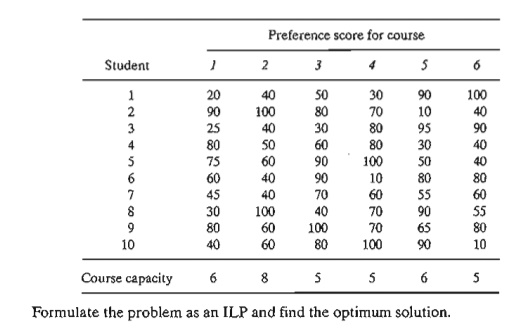
*12. (Graves and Associates, 1993) Ulem University uses a mathematical model that optimizes student preferences taking into account the limitation of classroom and faculty re-sources. To demonstrate the application of the model, consider the simplified case of 10 students who are required to select two courses out of six offered electives. The table below gives scores that represent each student's preference for individual courses, with a score of 100 being the highest. For simplicity, it is assumed that the preference score for a two-course selection is the sum of the individual score. Course capacity is the maximum number of students allowed to take the class.