Chapter: civil : Applied Hydraulic Engineering: Uniform Flow
Best Hydraulic Cross- Section
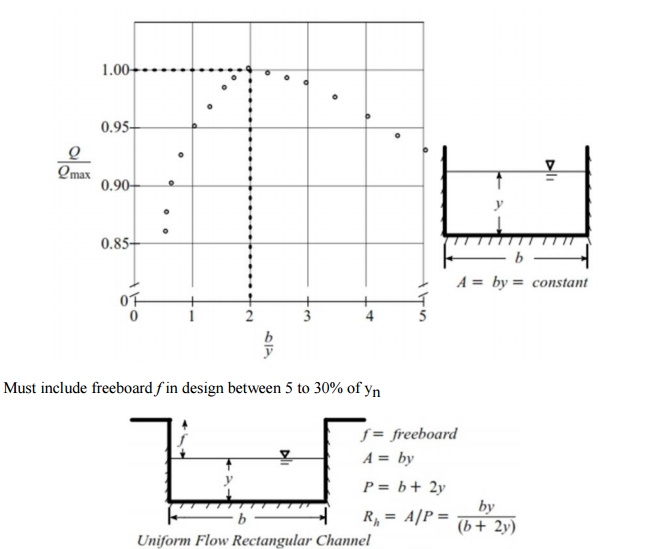
Best Hydraulic Cross- Section
We often want to know the the minimum area A for a
given flow Q, slope S0 and roughness coef- ficient n.
This is
known as the best hydraulic cross section
The
quantity ARh2/3 in Mannings' equation
is called the section factor
Writing
the Manning equation with Rh = A/P, we get
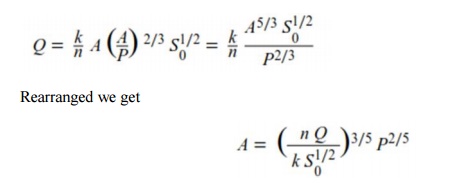
·
( inside ) is a constant; Channel with minimum A is also minimum P
·
Minimum excavation area A also has minimum P
·
Best possible is semicircular channel, but
construction costs are high
Let's find out what the
best hydraulic cross section is for a rectan- gular channel
Example: Water
flows uniformly in a rectangular channel of width b and depth y. Determine the
aspect ratio b/y for the best hydraulic cross section.

·
Thus best hydraulic cross- section for a
rectangular channel occurs when the depth is one-half the width of the channel
· Note for
1 < b/y < 4; Q ˜
.96 Qmax
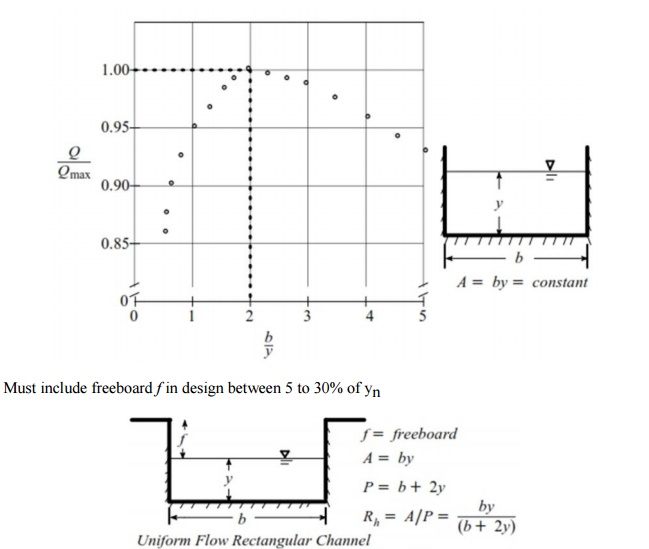
Must include freeboard f in design between 5 to 30% of
yn
Table gives Optimum properties of Open Channel Sections
.For trapezoid, half- hexagon
.For circular section, half- circle
.For triangular section, half- square
Design of Erodible Channels
Design velocity V small enough not to cause erosion
Find maximum permissible velocity based on channel material
(Roberson, Table 4- 3)
Maximum
Permissible Velocities a nd n Values for
Different Materials
Material V(ft/s) n
Fine Sand 1.50 0.020
Sandy loam 1.75 0.020
Silt loam 2.00 0.020
Firm loam 2.50 0.020
Stiff clay 3.75 0.025
Fine gravel 2.50 0.025
Coarse gravel 4.00 0.025
Assuming a trapezoidal channel, maximum side slopes
depend on material (Roberson,Table 4-2)
Maximum Channel Wall Slopes for Different Materials
Material
: Side Slopes
Rock : Almost Vertical
Stiff clay or earth with concrete : 1/2 : 1 to 1:1
Firm Soil 1:1
Loose sandy soil 2:1
Sandy loam soil 3:1
Once Q, V, n, S0 are determined, solve
for depth y and width b.
Problem: For an unlined trapezoidal
irrigation canal in firm loam soil, slope is 0.0006 and flow is 100 cfs,
what dimensions?
For side slope, pick slope of 1 1/2 (h): 1 (v) (conservative)
Vmax = 2.5 ft/s, n = 0.020
To find Rh
To construct choose b = 18 ft and y = 2.0 ft.
Critical Slope
·
Holding n and Q constant, changing slope slope
will change depth and velocity
·
Where velocity and depth give a Froude number =1,
this is defined as the critical slope Sc and crit- ical depth yc
Related Topics