Why Algorithmic Complexity Is Important

Why Algorithmic Complexity Is Important

Algorithmic complexity represents the expected performance of a section of code as the number of elements being processed increases. In the limit, the code with the greatest algorithmic complexity will dominate the runtime of the application.

Assume that your application has two regions of code, one that is O(N) and another that is O(N²). If you run a test workload of 100 elements, you may find that the O(N) code takes longer to execute, because there may be more instructions associated with the computation on each element. However, if you were to run a workload of 10,000 ele-ments, then the more complex routine would start to show up as important, assuming it did not completely dominate the runtime of the application.

Picking a small workload will mislead you as to which parts of the code need to be optimized. You may have spent time optimizing the algorithmically simpler part of the code, when the performance of the application in a real-world situation will be domi-nated by the algorithmically complex part of the code. This emphasizes why it is impor-tant to select appropriate workloads for developing and testing the application. Different parts of the application will scale differently as the workload size changes, and regions that appear to take no time can suddenly become dominant.

Another important point to realize is that a change of algorithm is one of the few things that can make an order of magnitude difference to performance. If 80% of the application’s runtime was spent sorting a 1,000-element array, then switching from a bubble sort to a quicksort could make a 300× difference to the performance of that function, making the time spent sorting 300× smaller than it previously was. The 80% of the runtime spent sorting would largely disappear, and the application would end up running about five times faster.

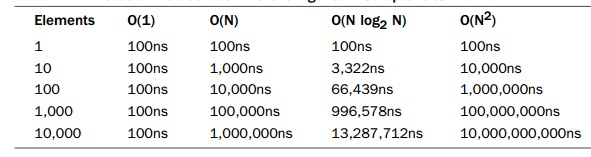
Table 2.1 shows the completion time of a task with different algorithmic complexities as the number of elements grows. It is assumed that the time to complete a single unit of work is 100ns. As the table illustrates, it takes remarkably few elements for an O(N²) algorithm to start consuming significant amounts of time.

Table 2.1      Execution Duration at Different Algorithm Complexities

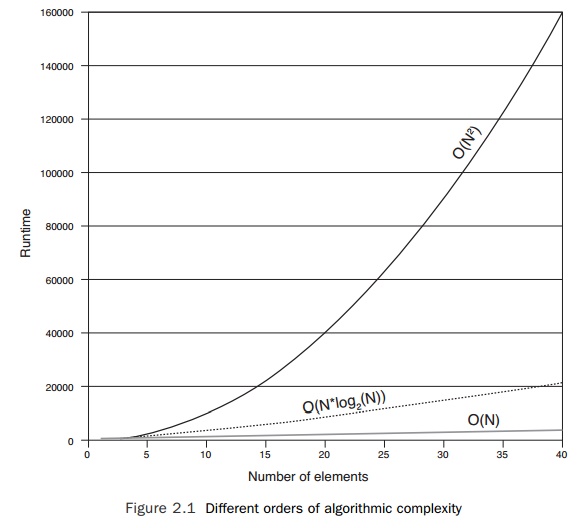
The same information can be presented as a chart of runtimes versus the number of elements. Figure 2.1 makes the same point rather more dramatically. It quickly becomes apparent that the runtime for an O(N²) algorithm will be far greater than one that is linear or logarithmic with respect to the number of elements.