Chapter: Physics : Electromagnetic Waves and Wave optics : Higher Secondary(12 Std)
Wave front
Wave front
When a stone is dropped in a still water, waves spread out along the surface of water in all directions with same velocity. Every particle on the surface vibrates. At any instant, a photograph of the surface of water would show circular rings on which the disturbance is maximum (Fig. 5.8).

It is clear that all the particles on such a circle are vibrating in phase, because these particles are at the same distance from the source. Such a surface which envelopes the particles that are in the same state of vibration is known as a wave front. The wave front at any instant is defined as the locus of all the particles of the medium which are in the same state of vibration.
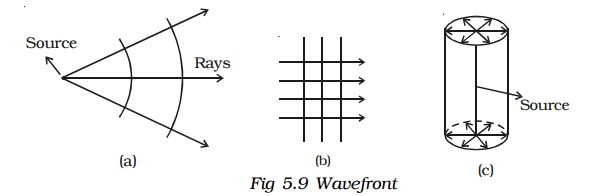
A point source of light at a finite distance in an isotropic medium* emits a spherical wave front (Fig 5.9a). A point source of light in an isotropic medium at infinite distance will give rise to plane wavefront (Fig. 5.9b). A linear source of light such as a slit illuminated by a lamp, will give rise to cylindrical wavefront (Fig 5.9c).
1. Huygen’s principle
Huygen’s principle helps us to locate the new position and shape of the wavefront at any instant, knowing its position and shape at any previous instant. In other words, it describes the progress of a wave front in a medium.
Huygen’s principle states that, (i) every point on a given wave front may be considered as a source of secondary wavelets which spread out with the speed of light in that medium and (ii) the new wavefront is the forward envelope of the secondary wavelets at that instant.
Huygen’s construction for a spherical and plane wavefront is shown in Fig. 5.10a. Let AB represent a given wavefront at a time t = 0. According to Huygen’s principle, every point on AB acts as a source of secondary wavelets which travel with the speed of light c. To find the position of the wave front after a time t, circles are drawn with points P, Q, R ... etc as centres on AB and radii equal to ct. These are the traces of secondary wavelets. The arc A1B1 drawn as a forward envelope of the small circles is the new wavefront at that instant. If the source of light is at a large distance, we obtain a plane wave front A1 B1 as shown in Fig 5.10b.

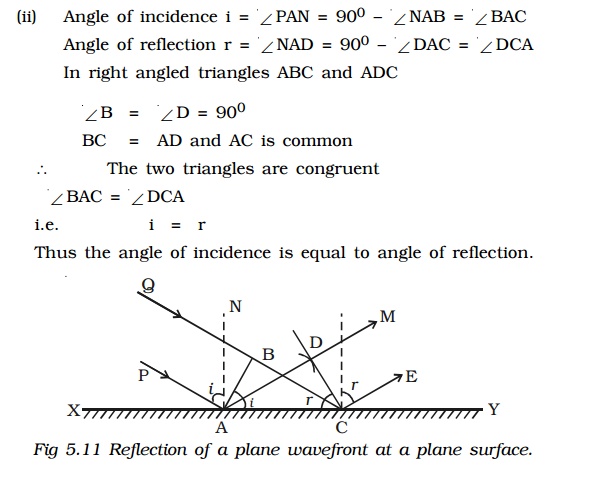
2 Reflection of a plane wave front at a plane surface
Let XY be a plane reflecting surface and AB be a plane wavefront incident on the surface at A. PA and QBC are perpendiculars drawn to AB at A and B respectively. Hence they represent incident rays. AN is the normal drawn to the surface. The wave front and the surface are perpendicular to the plane of the paper (Fig. 5.11).
According to Huygen’s principle each point on the wavefront acts as the source of secondary wavelet. By the time, the secondary wavelets from B travel a distance BC, the secondary wavelets from A on the reflecting surface would travel the same distance BC after reflection. Taking A as centre and BC as radius an arc is drawn. From C a tangent CD is drawn to this arc. This tangent CD not only envelopes the wavelets from C and A but also the wavelets from all the points between C and A. Therefore CD is the reflected plane wavefront and AD is the reflected ray.
Laws of reflection
(i) The incident wavefront AB, the reflected wavefront CD and the reflecting surface XY all lie in the same plane.
3. Refraction of a plane wavefront at a plane surface
Let XY be a plane refracting surface separating two media 1 and 2 of refractive indices µ1 and µ2 (Fig 5.12). The velocities of light in these two media are respectively c1 and c2. Consider a plane wave front AB incident on the refracting surface at A. PA and QBC are perpendiculars drawn to AB at A and B respectively. Hence they represent incident rays. NAN1 is the normal drawn to the surface. The wave front and the surface are perpendicular to the plane of the paper.
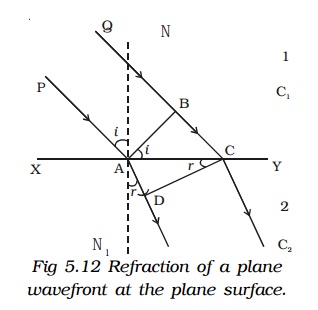
According to Huygen’s principle each point on the wave front act as the source of secondary wavelet. By the time, the secondary wavelets from B, reaches C, the secondary wavelets from the point A would travel a distance AD = C2t, where t is the time taken by the wavelets to travel the distance BC.
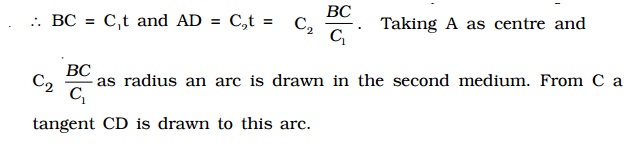
This tangent CD not only envelopes the wavelets from C and A but also the wavelets from all the points between C and A. Therefore CD is the refracted plane wavefront and AD is the refracted ray.
Laws of refraction
(i) The incident wave front AB, the refracted wave front CD and the refracting surface XY all lie in the same plane.


4. Total internal reflection by wave theory
Let XY be a plane surface which separates a rarer medium (air) and a denser medium. Let the velocity of the wavefront in these media be Ca and Cmrespectively.
A plane wavefront AB passes from denser medium to rarer medium. It is incident on the surface with angle of incidence i. Let r be the angle of refraction.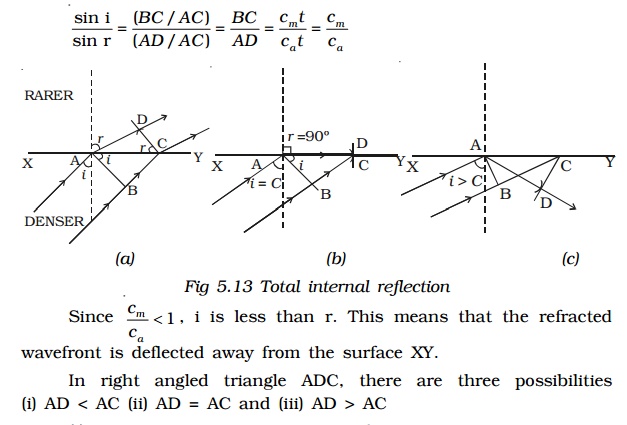
(ii) AD = AC : As i increases r also increases. When AD = AC, sin r = 1 (or) r = 900. i.e a refracted wavefront is just possible (Fig. 5.13b). Now the refracted ray grazes the surface of separation of the two media. The angle of incidence at which the angle of refraction is 900 is called the critical angle C.
(iii) AD > AC : When AD > AC, sin r > 1. This is not possible (Fig 5.13c). Therefore no refracted wave front is possible, when the angle of incidence increases beyond the critical angle. The incident wavefront is totally reflected into the denser medium itself. This is called total internal reflection.
Hence for total internal reflection to take place (i) light must travel from a denser medium to a rarer medium and (ii) the angle of incidence inside the denser medium must be greater than the critical angle. i.e i > C.
Related Topics