Volume of Cuboid and Cube

Volume of Cuboid and Cube

All of us have tasted 50 ml and 100 ml of ice cream. Take one such 100 ml ice cream cup. This cup can contain 100 ml of water, which means that the capacity or volume of that cup is 100 ml. Take a 100 ml cup and find out how many such cups of water can fill a jug. If 10 such 100 ml cups can fill a jug then the capacity or volume of the jug is 1 litre (10 Ã— 100ml = 1000ml = 1l). Further check how many such jug of water can fill a bucket. That is the capacity or volume of the bucket. Likewise we can calculate the volume or capacity of any such things.

Volume is the measure of the amount of space occupied by a three dimensional solid.

Cubic centimetres ( cm3) , cubic metres (m3) are some cubic units to measure volume.

Volume of the solid is the product of ‘base area’ and ‘height’. This can easily be understood from a practical situation. You might have seen the bundles of A4 size paper. Each paper is rectangular in shape and has an area (=lb). When you pile them up, it becomes a bundle in the form of a cuboid; h times lb make the cuboid.

1. Volume of a Cuboid

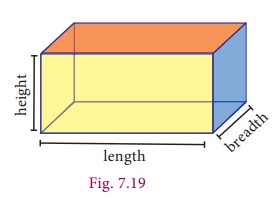
Let the length, breadth and height of a cuboid be l, b and h respectively.

Then, volume of the cuboid

V = (cuboid’s base area) Ã— height

= (l Ã— b) Ã— h = lbh cubic units

Note

The units of length, breadth and height should be same while calculating the volume of a cuboid.

Example 7.9

The length, breadth and height of a cuboid is 120 mm, 10 cm and 8 cm respectively. Find the volume of 10 such cuboids.

Solution

Since both breadth and height are given in cm, it is necessary to convert the length also in cm.

So we get, l = 120 mm = 120/10 = 12 cm and take b = 10 cm, h = 8 cm as such.

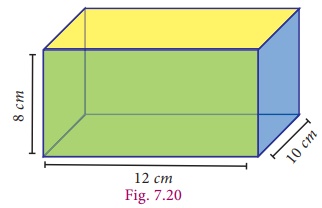
Volume of a cuboid = l × b × h

=12×10×8

= 960 cm3

Volume of 10 such cuboids = 10 Ã— 960

= 9600 cm3

Example 7.10

The length, breadth and height of a cuboid are in the ratio 7:5:2. Its volume is 35840 cm3. Find its dimensions.

Solution

Let the dimensions of the cuboid be

 l= 7x, b = 5x and h = 2x.

Given that volume of cuboid = 35840 cm3

l Ã— b Ã— h = 35840

(7x)(5x)(2x) = 35840

70x3 = 35840

x3 = 35840/70

x3 = 512

 x = 3√[8 × 8 × 8]

 x= 8 cm

Length of cuboid = 7x = 7 Ã— 8 = 56cm

Breadth of cuboid = 5x = 5 Ã— 8 = 40cm

Height of cuboid = 2x = 2 Ã— 8 = 16 cm

Example 7.11

The dimensions of a fish tank are 3.8 m Ã— 2.5 m Ã— 1.6 m. How many litres of water it can hold?

Solution

Length of the fish tank l =3.8 m

Breadth of the fish tank b =2.5 m ,

Height of the fish tank h =1.6 m

Volume of the fish tank = l Ã— b Ã— h

= 3.8 Ã— 2.5 Ã—1.6

= 15.2 m3

= 15.2 Ã—1000 litres

= 15200 litres

Note

A few important conversions

1 cm3 =1 ml, 1000 cm3=1 litre, 1m3 =1000 litres

Example 7.12

The dimensions of a sweet box are 22 cm Ã— 18 cm Ã— 10 cm. How many such boxes can be packed in a carton of dimensions 1 m Ã— 88 cm Ã— 63 cm?

Solution

Here, the dimensions of a sweet box are Length (l) = 22cm, breadth (b) = 18cm, height (h) = 10 cm.

Volume of a sweet box = l Ã— b Ã— h

= 22 Ã—18 Ã—10 cm3

The dimensions of a carton are

Length (l) = 1m= 100 cm, breadth (b) = 88 cm, height (h) = 63 cm.

Volume of the carton = l Ã— b Ã— h

= 100 Ã— 88 Ã— 63 cm3

The number of sweet boxes packed = volume of the carton / volume of a sweet box

= [100×88×63] / [22 ×18 ×10]

= 140 boxes

THINKING CORNER

Each cuboid given below has the same volume 120 cm3. Can you find the missing dimensions?

2. Volume of a Cube

It is easy to get the volume of a cube whose side is a units. Simply put l = b = h = a in the formula for the volume of a cuboid. We get volume of cube to be a3 cubic units.

If the side of a cube is ‘a’ units then the Volume of the cube (V) = a3 cubic units.

Note

For any two cubes, the following results are true.

• Ratio of surface areas = (Ratio of sides)2

• Ratio of volumes = (Ratio of sides)3

• (Ratio of surface areas)3 = (Ratio of volumes)2

Example 7.13

Find the volume of cube whose side is 10 cm.

Solution

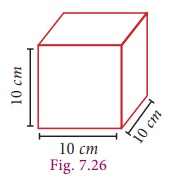
Given that side (a) = 10 cm

volume of the cube = a3

= 10 Ã—10 Ã—10

= 1000 cm3

Example 7.14

A cubical tank can hold 64,000 litres of water. Find the length of its side in metres.

Solution

Let ‘a’ be the side of cubical tank.

Here, volume of the tank = 64,000 litres

i.e., a3 = 64,000 = 64000/1000 [since,1000 litres=1m3 ]

a3 = 64 m3

a = 3√64 a = 4 m

Therefore, length of the side of the tank is 4 metres.

Example 7.15

The side of a metallic cube is 12 cm. It is melted and formed into a cuboid whose length and breadth are 18 cm and 16 cm respectively. Find the height of the cuboid.

Solution

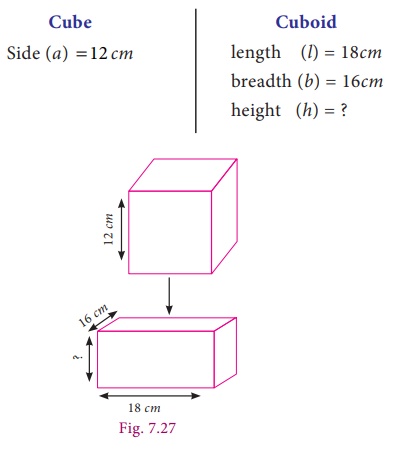
Here, Volume of the Cuboid = Volume of the Cube

 l× b Ã— h = a3

 18 Ã— 16 Ã— h = 12 Ã—12 Ã—12

h = 12 ×12 ×12 / 18 ×16

h = 6 cm

Therefore, the height of the cuboid is 6 cm.

Activity

Take some square sheets of paper / chart paper of given dimension 18 cm Ã— 18 cm. Remove the squares of same sizes from each corner of the given square paper and fold up the flaps to make a open cuboidal box. Then tabulate the dimensions of each of the cuboidal boxes made. Also find the volume each time and complete the table. The side measures of corner squares that are to be removed is given in the table below.

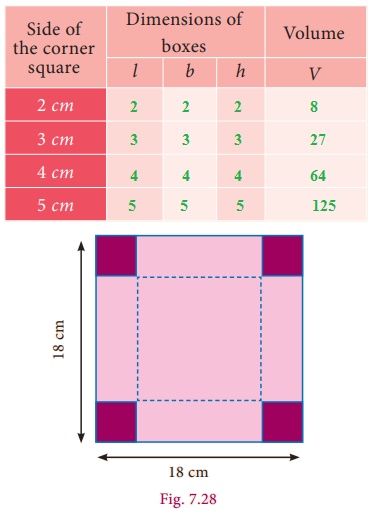
Observe the above table and answer the following:

(i) What is the greatest possible volume? Volume: 9x9x9=729 cm3 / 18x18x18=5832 cm3

(ii) What is the side of the square that when removed produces the greatest volume? Side: 9cm / 18cm