Surface Area of Cuboid and Cube

Surface Area of Cuboid and Cube

We have learnt in the earlier classes about 3-Dimension structures. The 3D shapes are those which do not lie completely in a plane. Any 3D shape has dimensions namely length, breadth and height.

1. Cuboid and its Surface Area

Cuboid: A cuboid is a closed solid figure bounded by six rectangular plane regions. For example, match box, Brick, Book.

A cuboid has 6 faces, 12 edges and 8 vertices. Ultimately, a cuboid has the shape of a rectangular box.

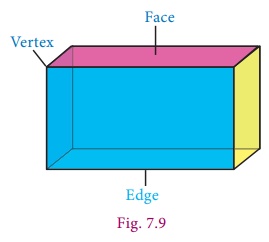
Total Surface Area (TSA) of a cuboid is the sum of the areas of all the faces that enclose the cuboid. If we leave out the areas of the top and bottom of the cuboid we get what is known as its Lateral Surface Area (LSA).

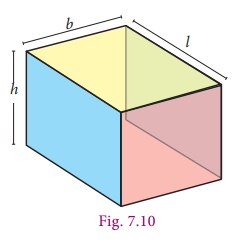
In the Fig 7.10, l, b and h represents length, breadth and height respectively.

(i) Total Surface Area (TSA) of a cuboid

 = 2 (lb + bh + lh ) sq. units.

(ii) Lateral Surface Area (LSA) of a cuboid

 = 2 (l+b)h sq. units.

We are using the concept of Lateral Surface Area (LSA) and Total Surface Area (TSA) in real life situations. For instance a room can be cuboidal in shape that has different length, breadth and height. If we require to find areas of only the walls of a room, avoiding floor and ceiling then we can use LSA. However if we want to find the surface area of the whole room then we have to calculate the TSA.

If the length, breadth and height of a cuboid are l, b and h respectively. Then

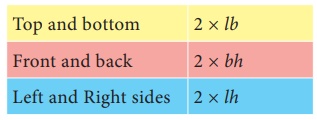
(i) Total Surface Area = 2 (lb + bh + lh ) sq.units.

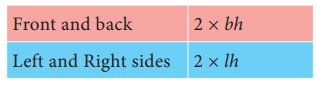
(ii) Lateral Surface Area = 2 (l+b)h sq.units.

Note

• The top and bottom area in a cuboid is independent of height. The total area of top and bottom is 2lb. Hence LSA is obtained by removing 2lb from 2(lb+bh+lh).

• The units of length, breadth and height should be same while calculating surface area of the cuboid.

Example 7.4

Find the TSA and LSA of a cuboid whose length, breadth and height are 7.5 m, 3 m and 5 m respectively.

Solution

Given the dimensions of the cuboid;

that is length (l) = 7.5 m, breadth (b) = 3 m and height (h) = 5 m.

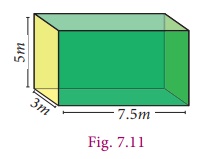
TSA = 2(lb + bh + lh)

= 2[(7.5 × 3) + (3 × 5) + (7.5 × 5)]

= 2(22.5 +15 + 37.5)

= 2×75

= 150 m²

LSA = 2(l + b) × h

=2(7.5+3)×5

=2×10.5×5

= 105 m²

Example 7.5

The length, breadth and height of a hall are 25 m, 15 m and 5 m respectively. Find the cost of renovating its floor and four walls at the rate of ₹80 per m².

Solution

Here, length (l ) = 25 m, breadth (b) =15 m, height (h) = 5 m.

Area of four walls = LSA of cuboid

= 2(l + b) × h

= 2(25 +15) × 5

= 80 × 5 = 400 m²

Area of the floor = l × b

= 25 ×15

= 375 m²

Total renovating area of the hall

= (Area of four walls + Area of the floor)

= (400 + 375) m²

= 775 m²

Therefore, cost of renovating at the rate of ₹80 per m² = 80 × 775

= ₹ 62,000

2. Cube and its Surface Area

Cube: A cuboid whose length, breadth and height are all equal is called as a cube.

That is a cube is a solid having six square faces. Here are some real-life examples.

A cube being a cuboid has 6 faces, 12 edges and 8 vertices.

Consider a cube whose sides are ‘a’ units as shown in the Fig 7.14. Now,

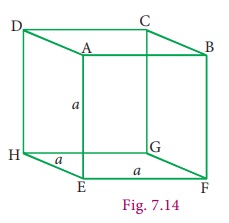
(i) Total Surface Area of the cube

= sum of area of the faces (ABCD+EFGH+AEHD+BFGC+ABFE+CDHG)

= (a ² + a ² + a ² + a ² + a ² + a² )

= 6a² sq. units

(ii) Lateral Surface Area of the cube

= sum of area of the faces (AEHD+BFGC+ABFE+CDHG)

= (a ² + a ² + a ² + a² )

= 4a² sq. units

If the side of a cube is a units, then,

(i) The Total Surface Area = 6a² sq.units

(ii) The Lateral Surface Area = 4a² sq.units

Thinking Corner: Can you get these formulae from the corresponding formula of Cuboid?

Example 7.6

Find the Total Surface Area and Lateral Surface Area of the cube, whose side is 5 cm.

Solution

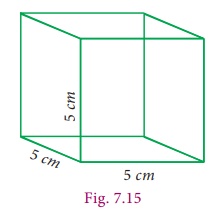
The side of the cube (a) = 5 cm

Total Surface Area = 6a² = 6(5² ) = 150 sq. cm

Lateral Surface Area = 4a² = 4(5² ) = 100 sq. cm

Example 7.7

A cube has the Total Surface Area of 486 cm². Find its lateral surface area.

Solution

Here, Total Surface Area of the cube = 486 cm²

6a² = 486 ⇒ a² = 486/6 and so, a² = 81 . This gives a = 9.

The side of the cube = 9 cm

Lateral Surface Area = 4a² = 4 × 9² = 4 × 81 = 324 cm²

Example 7.8

Two identical cubes of side 7 cm are joined end to end. Find the Total and Lateral surface area of the new resulting cuboid.

Solution

Side of a cube = 7 cm

Now length of the resulting cuboid (l) = 7+7 =14 cm

Breadth (b) = 7 cm, Height (h) = 7 cm

So, Total Surface Area = 2(lb + bh + lh)

= 2 [(14×7)+(7×7)+(14×7)]

= 2(98 + 49 + 98)

=2×245

= 490 cm²

Lateral Surface Area = 2(l + b) × h

= 2(14+7)×7 =2×21×7

= 294 cm²