Application of Heron’s Formula in Finding Areas of Quadrilaterals

Application of Heron’s Formula in Finding Areas of Quadrilaterals

A plane figure bounded by four line segments is called a quadrilateral.

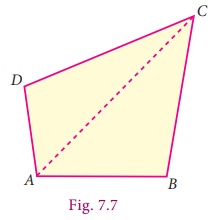
Let ABCD be a quadrilateral. To find the area of a quadrilateral, we divide the quadrilateral into two triangular parts and use Heron’s formula to calculate the area of the triangular parts.

In Fig 7.7,

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD

Example 7.3

A farmer has a field in the shape of a rhombus. The perimeter of the field is 400m and one of its diagonal is 120m. He wants to divide the field into two equal parts to grow two different types of vegetables. Find the area of the field.

Solution

Let ABCD be the rhombus.

Its perimeter = 4 × side = 400 m

Therefore, each side of the rhombus = 100 m

Given the length of the diagonal AC = 120 m

In ∆ABC, let a =100 m, b =100 m, c =120 m

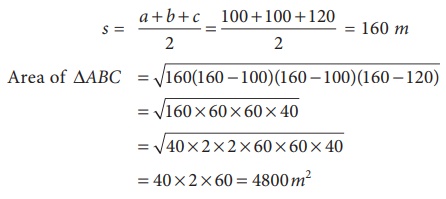
 s = (a + b + c) / 2 = (100 +100 +120) / 2 = 160 m

Area of ΔABC = √ [160(160 −100)(160 −100)(160 −120)]

= √ [160×60×60×40]

= √ [40×2×2×60×60×40]

= 40 × 2 × 60 = 4800m²

Therefore, Area of the field ABCD = 2 × Area of ABC = 2 × 4800 = 9600 m²