Mensuration | Maths - HeronŌĆÖs Formula | 9th Maths : UNIT 7 : Mensuration
Chapter: 9th Maths : UNIT 7 : Mensuration
HeronŌĆÖs Formula
HeronŌĆÖs Formula
How will
you find the area of a triangle, if the height is not known but the lengths of the
three sides are known?
For this,
Heron has given a formula to find the area of a triangle.
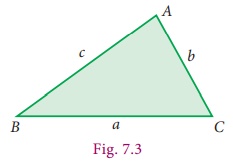
If a, b and c are the sides of a triangle, then the
area of a triangle = ŌłÜ[ s ( s ŌłÆ a )(s ŌłÆ b)(s ŌłÆ c)] sq.units.
where s = [ a + b + c ]
/ 2, ŌĆśsŌĆÖ is the semi-perimeter (that is half of the perimeter) of the triangle.
Note
If we assume that the sides are of equal length that is a
= b = c, then HeronŌĆÖs formula will be ŌłÜ3/4 a2 sq.units, which
is the area of an equilateral triangle.
Example 7.1
The lengths
of sides of a triangular field are 28 m, 15 m and 41 m. Calculate
the area of the field. Find the cost of levelling the field at the rate of Ōé╣ 20
per m2.
Solution
Let a = 28 m, b = 15 m and c = 41m
Then, s = (a + b + c) /
2 = (28 +15+ 41) / 2 = 84/2 = 42 m
Area of triangular field = ŌłÜ [ s(s ŌłÆ a)(s ŌłÆ b)(s ŌłÆ c)
]
= ŌłÜ [ 42(42 ŌłÆ 28)(42 ŌłÆ15)(42 ŌłÆ 41)]
= ŌłÜ [42 ├Ś14 ├Ś 27 ├Ś1]
= ŌłÜ [ 2├Ś3├Ś7├Ś7├Ś2├Ś3├Ś3├Ś3├Ś1]
= 2├Ś3├Ś7├Ś3
= 126 m2
Given the
cost of levelling is Ōé╣ 20 per m2.
The total
cost of levelling the field = 20 ├Ś126 = Ōé╣ 2520.
Example 7.2
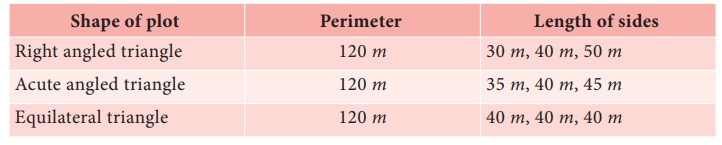
Three different
triangular plots are available for sale in a locality. Each plot has a perimeter
of 120 m. The side lengths are also given:
Help the
buyer to decide which among these will be more spacious.
Solution
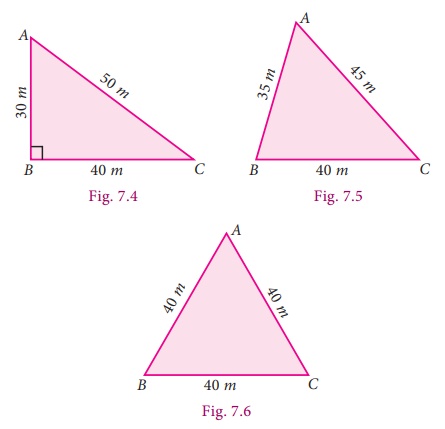
For clarity,
let us draw a rough figure indicating the measurements:
(i) The semi-perimeter of
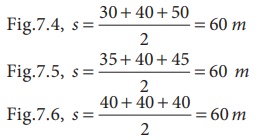
Note that
all the semi-perimeters are equal.
(ii) Area
of triangle using HeronŌĆÖs formula:
In Fig.7.4,
Area of triangle = ŌłÜ [60(60 ŌłÆ 30)(60 ŌłÆ 40)(60 ŌłÆ 50)]
= ŌłÜ [60├Ś30├Ś20├Ś10]
= ŌłÜ [30├Ś2├Ś30├Ś2├Ś10├Ś10]
= 600 m2
In Fig.7.5,
Area of triangle = ŌłÜ [60(60 ŌłÆ 35)(60 ŌłÆ 40)(60 ŌłÆ 45)]
= ŌłÜ [60├Ś25├Ś20├Ś15]
= ŌłÜ [20├Ś3├Ś5├Ś5├Ś20├Ś3├Ś5]
= 300 ŌłÜ5
( Since ŌłÜ5 = 2.236 )
= 670.8 m2
In Fig.7.6,
Area of triangle = ŌłÜ [60(60 ŌłÆ 40)(60 ŌłÆ 40)(60 ŌłÆ 40)]
= ŌłÜ [60├Ś20├Ś20├Ś20]
= ŌłÜ [3├Ś20├Ś20├Ś20├Ś20]
= 400 ŌłÜ3
( Since ŌłÜ3 = 1.732 )
= 692.8 m2
We find that
though the perimeters are same, the areas of the three triangular plots are different.
The area of the triangle in Fig 7.6 is the greatest among these; the buyer can be
suggested to choose this since it is more spacious.
Note
If the perimeter of different types of triangles have the same value,
among all the types of triangles, the equilateral triangle possess the greatest
area. We will learn more about maximum areas in higher classes.
Related Topics