Chapter: Theory of Computation
Unsolvable Problems And Computable
UNSOLVABLE PROBLEMS AND COMPUTABLE
Design a Turing machine to add two given integers.
Solution:

Some unsolvable Problems are as follows:
(i) Does a given Turing machine M halts on all input?
(ii) Does Turing machine M halt for any input?
(iii) Is the language L(M) finite?
(iv) Does L(M) contain a string of length k, for some given k?
(v) Do two Turing machines M1 and M2 accept the same language?
It is very obvious that if there is no algorithm that decides, for an arbitrary given Turing machine M and input string w, whether or not M accepts w. These problems for which no algorithms exist are called “UNDECIDABLE” or “UNSOLVABLE”.
Code for Turing Machine:



Proof that Ld is not recursively enumerable:

Recursive Languages:


Universal Language:

Undecidability of Universal Language:


Problem -Reduction : If P1 reduced to P2,
Then P2 is at least as hard as P1. Theorem: If P1 reduces to P2 then,
• If P1 is undecidable the so is P2.
• If P1 is Non-RE then so is P2.
Post' s Correspondence Problem ( PCP)




Proof: The halting problem of turning machine can be reduced to PCP to show the undecidability of PCP. Since halting problem of TM is undecidable (already proved), This reduction shows that PCP is also undecidable. The proof is little bit lengthy and left as an exercise.
Some undecidable problem in context-free languages
We can use the undecidability of PCP to show that many problem concerning the context-free languages are undecidable. To prove this we reduce the PCP to each of these problem. The following discussion makes it

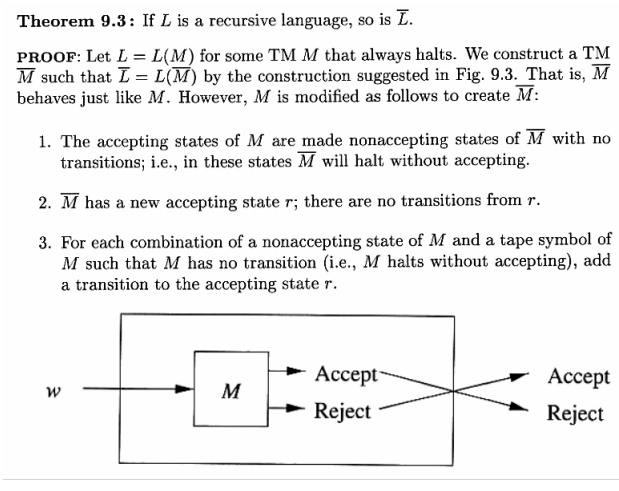
it is clear that the grammar Gx generates the strings that can appear in the LHS of a sequence while solving the PCP followed by a sequence of numbers. The sequence of number at the end records the sequence strings from the PCP instance (in reverse order) that generates the string. Gy generates the strings that can be obtained from the RHS of a sequence and the corresponding sequence of numbers (in reverse order).
Now, if the Post Correspondence System has a solution, then there must be a sequence


Proof: Assume for contradiction that there exists an algorithm A to decide this question. This would imply that
For any Post Correspondence System, P construct grammars G(x)and G(y) by using the constructions elaborated already. We can now use the algorithm A to decide whether and




i.e. iff the PCP instance has no solutions as discussed in part (ii).
Hence the proof.
Theorem : It is undecidable whether an arbitrary CFG is
Proof : Consider an arbitrary instance of PCP and construct the Gx and Gy and from the ordered pairs of CFG's
We construct a new grammar G from Gx and Gy as follows.
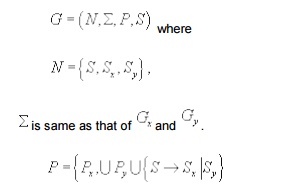
This constructions gives a reduction of PCP to
the -------- of whether a CFG is ambiguous, thus leading to the undecidability
of the given problem. That is, we will now show that the PCP has a solution if
and only if G is only if Assume that I1,I2,…Ik
is a solution sequence to this instance
of PCP.
Consider the following two derivation in I1,I2,…Ik
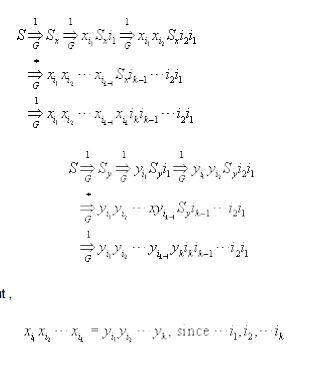


Non deterministic polynomial time:
• NP is the set of languags that are accepted by polynomial time NTM’s
• Many problems are in NP but appear not to be in p.
• One of the great mathematical questions of our age: is there anything in NP that is not in
NP-complete problems:
If We cannot resolve the “p=np question, we can at least demonstrate that certain problems in NP are
• These are called NP-complete.
• Intellectual leverage: Each NP-complete problem’s apparent difficulty reinforces the belief that they are all hard.
Methods for proving NP-Complete problems:
• Polynomial time reduction (PTR): Take time that is some polynomial in the input size to
• convert instances of one problem to instances of another.
• If P1 PTR to P2 and P2 is in P1 the so is P1.
• Start by showing every problem in NP has a PTR to Satisfiability of Boolean formula. Then, more problems can be proven NP complete by showing that SAT
Related Topics