Finite Automata

FINITE AUTOMATA

What is TOC?

In theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm. The field is divided into three major branches: automata theory, computability theory and computational complexity theory.

In order to perform a rigorous study of computation, computer scientists work with a mathematical abstraction of computers called a model of computation. There are several models in use, but the most commonly examined is the Turing machine.

Automata theory

In theoretical computer science, automata theory is the study of abstract machines (or more appropriately, abstract 'mathematical' machines or systems) and the computational problems that can be solved using these machines. These abstract machines are called automata.

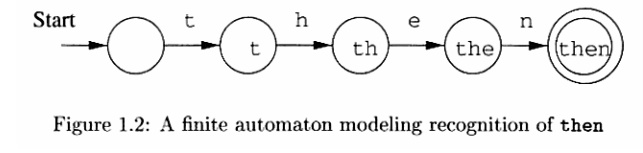
This automaton consists of

•      states (represented in the figure by circles),

As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function (which takes the current state and the recent symbol as its inputs).

Uses of Automata: compiler design and parsing.

Additive inverse: a+(-a)=0

Multiplicative inverse: a*1/a=1

Universal set U={1,2,3,4,5}

Subset A={1,3}

A’ ={2,4,5}

Absorption law: AU(A ∩B) = A, A∩(AUB) = A

De Morgan’s Law:

(AUB)’ =A’ ∩ B’ (A∩B)’ = A’ U B’ Double compliment

(A’)’ =A

A ∩ A’ = Φ

Logic relations: a b = > 7a U b 7(a∩b)=7a U 7b

Relations:

Let a and b be two sets a relation R contains aXb. Relations used in TOC:

Reflexive: a = a

Symmetric: aRb = > bRa

Transition: aRb, bRc = > aRc

If a given relation is reflexive, symmentric and transitive then the relation is called equivalence relation.

Deductive proof: Consists of sequence of statements whose truth lead us from some initial

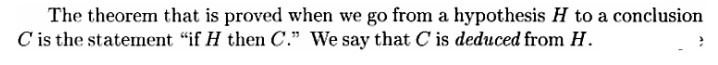
Additional forms of proof:

Proof of sets

Proof by contradiction

Proof by counter example

Direct proof (AKA) Constructive proof:

If p is true then q is true

Eg: if a and b are odd numbers then product is also an odd number. Odd number can be represented as 2n+1

a=2x+1, b=2y+1

product of a X b = (2x+1) X (2y+1)

= 2(2xy+x+y)+1 = 2z+1 (odd number)

Proof by contrapositive:

The contrapositive o the statement “if H and C” is “if not C then not H.” A statement and its contrapositive are either both true or both false, so we can prove either to prove the other.

Figure 1.6: Steps in the “only-if” part of Theorem 1.10

To see why “If H then C” and “I not C then not H” are logically equivalent, first observe that there are four cases to consider:

1. H and C both true

2. H true and C false

3. C true and H false

4. H and C both false

Proof by Contradiction:

H and not C implies falsehood.

That is, start by assuming both the hypothesis H and the negation of the conclusion C. Complete the proof by showing that something known to be false follows logically from H and not C. This form of proof is called proof by contradiction.

It often is easier to prove that a statement is not a theorem than to prove it is a theorem. As we mentioned, if S is any statement, then the statement “S is not a theorem” is itsel a statement without parameters, and thus can be regarded as an observation than a

Alleged Theorem : All primes are odd. (More formally, we might say: if integer x is a prime, then x is odd.)

DISPROOF: The integer 2 is a prime, but 2 is even.

Proof by mathematical Induction:

Languages :

The languages we consider for our discussion is an abstraction of natural languages. That is, our focus here is on formal languages that need precise and formal definitions. Programming languages belong to this category.

Symbols :

Symbols are indivisible objects or entity that cannot be defined. That is, symbols are atoms of the world of languages. A symbol is any single object such as ↑ , a, 0, 1, #, begin, or do. Usually, characters from a typical keyboard are only used as symbols.

Alphabets :

An alphabet is a finite, nonempty set of symbols. The alphabet of a language is denoted by ∑. When more than one alphabets are considered for discussion, subscripts may be used (e.g. ∑1, ∑2 etc) or sometimes other symbol like G may also be introduced.

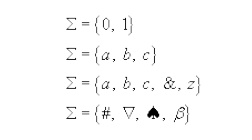
Example :

Strings or Words over Alphabet :

A string or word over an alphabet ∑ is a finite sequence of concatenated symbols   ∑.

Example : 0110, 11, 001 are three strings over the binary alphabet { 0, 1 }

aab, abcb, b, cc are four strings over the alphabet { a, b, c }

It is not the case that a string over some alphabet should contain all the symbols from the alphabet. For example, the string cc over the alphabet { a, b, c } does not contain the symbols a and b. Hence, it is true that a string over an alphabet is also a string over an alphabet is also a string over any superset of that alphabet.

Length of a string :

The number of symbols in a string w is called its length, denoted by | w|

Example : | 011 | = 4, |11| = 2, | b | = 1

Convention : We will use small case letters towards the beginning of the English alphabet to denote symbols of an alphabet and small case letters towards the end denote strings over an alphabet. That   a,b,c, Îå   (symbols) and u, v, w, x, y,z  are strings. 

Some String Operations :

Example : Consider the string 011 over the binary alphabet. All the prefixes, suffixes

Prefixes: ε, 0, 01, 011. Suffixes:

ε, 1, 11, 011. Substrings: ε, 0, 1, 01, 11, 011.

Note that x is a prefix (suffix or substring) to x, for any string x and ε is a prefix (suffix or substring) to any string.

A string x is a proper prefix (suffix) of string y if x is a prefix (suffix) of y and x ≠ y.

In the above example, all prefixes except 011 are proper

Powers of Strings : For any string x and n>=0, we use x pow(n) to denote the string formed by sequentially concatenating n copies of x. We can also give an

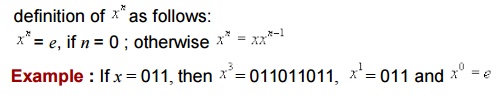
Powers of Alphabets :

We write åk (for some integer k) to denote the set of strings of length k with symbols from å . In other words,

åk = { w | w is a string over å and | w | = k}. Hence, for any alphabet, åo denotes the set of all strings of length zero. That åo= { e }. For the binary alphabet { 0, 1 } we is,

åo= {e}

å1= {0,1}

å2= {00,01,10,11}

å3= {000,001,010, 011,100, 101,110,111}

The set of all strings over an alphabet å is denoted by å*. That is,

å* = å0 U  å1 U å2 U……. åx U …….

=  U åk

The set å* contains all the strings that can be generated by iteratively symbols from any number of times.

Example : If  å = { a, b }, then = { ε, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, …}.

Convention : Capital letters A, B, C, L, etc. with or without subscripts are normally used

Set operations on languages : Since languages are set of strings we can apply set operations to languages. Here are some simple examples (though there is nothing new in it).

An automata is an abstract computing device (or machine). There are different varities

of such abstract machines (also called models of computation) which can be

Every Automaton fulfills the three basic

•         Every automaton consists of some essential features as in real computers. It has a mechanism for reading input. The input is assumed to be a sequence of symbols over a given alphabet and is placed on an input tape(or written on an input file). The simpler automata can only read the input one symbol at a time from left to right but not change. Powerful versions can both read

•         The automaton can produce output of some form. If the output in response to an input string is binary (say, accept or reject), then it is called an accepter. If it produces an output sequence in response to an input sequence, then it is called a transducer(or automaton with output).

•         The automaton may have a temporary storage, consisting of an unlimited number of cells, each capable of holding a symbol from an alphabet ( whcih may be different from the input alphabet). The automaton can both read and change the contents of the storage cells in the temporary storage. The accusing capability of this storage varies depending on the type of the storage.

•         The most important feature of the automaton is its control unit, which can be in any one of a finite number of interval states at any point. It can change state in some defined manner determined by a transition function.

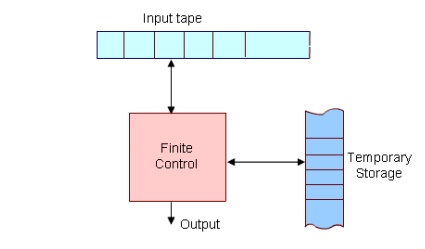
Figure 1: The figure above shows a diagrammatic representation of a generic automation.

Operation of the automation is defined as follows.

At any point of time the automaton is in some integral state and is reading a particular symbol from the input tape by using the mechanism for reading input. In the next time step the automaton then moves to some other integral (or remain in the same state) as defined by the transition function. The transition function is based on the current state, input symbol read, and the content of the temporary storage. At the same time the content of the storage may be changed and the input read may be modifed. The automation may also produce some output during this transition. The internal state, input and the content of storage at any point defines the configuration of the automaton at that point. The transition from one configuration to the next ( as defined by the transition function) is called a move. Finite state machine or Finite Automation is the simplest type of abstract machine we consider. Any system that is at any point of time in one of a finite number of interval state and moves among these states in a defined manner in response to some input, can be modeled by a finite automaton.

Finite Automata

Automata (singular : automation) are a particularly simple, but useful, model of computation. They were initially proposed as a simple model for the behavior of neurons.

States, Transitions and Finite - State Transition System :

Let us first give some intuitive idea about a state of a system and st at e before describing finite

Informally, a sta te o f a syste m is an instantaneous description of that system gives all relevant information necessary to determine how the system can evolve from T ran si t ions are changes of states that can occur spontaneously or in response to inputs to the states. Though transitions usually take time, we assume that state transitions

Some examples of state transition systems are: digital systems, vending machines,

A system containing only a finite number of states and transitions among them is called

Finite-state transition systems can be modeled abstractly by a mathematical model

Deterministic Finite (-state) Automata

Informally, a DFA (Deterministic Finite State Automaton) is a simple machine that reads an input string -- one symbol at a time -- and then, after the input has been completely read, decides whether to accept or reject the input. As the symbols are read from the tape, the automaton can change its state, to reflect how it reacts to what it has seen so far. A machine for which a deterministic code can be formulated, and if there is only one unique way to formulate the code, then the machine is called deterministic

Thus, a DFA conceptually consists of 3 parts:

 finite number of states that the machine is allowed to be in (zero or more states are designated as accept or final states), a state transition function for changing the current

An automaton processes a string on the tape by repeating the following actions until the

1. The tape head reads the current tape cell and sends the symbol s found there to the control. Then the tape head moves to the next cell.

2. The control takes s and the current state and consults the state transition

Once the entire string has been processed, the state in which the automation enters is examined. If it is an accept state , the input string is accepted ; otherwise, the string

Deterministic Finite State Automaton : A Deterministic Finite State Automaton (DFA) is a 5-tuple

Acceptance of Strings :

Language Accepted or Recognized by a DFA :

Extended transition function :

is the state the automation reaches when it starts from the state q finish processing the string w. Formally, we can give an inductive definition as 

The language of the DFA M is the set of strings that can take the start state to one of the accepting states i.e.

It is a formal description of a DFA. But it is hard to comprehend. 

We can describe the same DFA by transition table or state transition diagram as

Transition Table :

It is easy to comprehend the transition

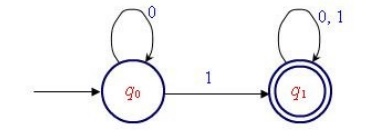
Explanation : We cannot reach find state  q1 w/0 or in the i/p string. There can be any no. of 0's at the beginning. ( The self-loop q0 on label 0 indicates it ). 

Transition table :

It is basically a tabular representation of the transition function that takes two arguments

•         Rows correspond to states,

•         Columns correspond to input symbols,

•         Entries correspond to next states

•         The start state is marked with an arrow

•         The accept states are marked with a star

(State) Transition diagram :

A state transition diagram or simply a transition diagram is a directed graph which can

1. For each state in Q there is a node.

2. There is a directed edge from node q to node p labeled a d (q.a)=p . (If there are several input symbols that cause a transition, the edge is labeled by the list of these symbols.)

3.       There is an arrow with no source into the start state.

5 .

6. Here is an informal description how a DFA operates. An input to a DFA can be any string  wÎå. Put a pointer to the start state q. Read the input string w left to right, one symbol at a time, moving the pointer according to the transition d  pointer to d(p,a) . When the end of the input string w is encountered, the is on some state, r. The string is said to be accepted by the DFA rÎF and rejected if ÏF. Note that there is no formal mechanism for moving the  A language LΠå* pointer.

Regular Expressions: Formal Definition

We construct REs from primitive constituents (basic elements) by repeatedly applying

Definition : Let S be an alphabet. The regular expressions are defined recursively as

Basis :

Language described by REs : Each describes a language (or a language is associated with every RE). We will see later that REs are used to attribute regular languages.

Notation : If r is a RE over some alphabet then L(r) is the language associate with r

Precedence Rule

Consider the RE ab + c. The language described by the RE can be thought of L(a)L(b+c) or L(ab)È L(c) as provided by the rules (of languages described by given already. But these two represents two different languages lending to ambiguity.

1)  Use fully parenthesized expression- (cumbersome)

2)  Use a set of precedence rules to evaluate the options of REs in some order. Like For REs, the order of precedence for the operators is as

i) The star operator precedes concatenation and concatenation precedes union (+)

ii) It is also important to note that concatenation & union (+) operators are associative

Using these precedence rule, we find that the RE ab+c represents the language L(ab)

We can, of course change the order of precedence by using parentheses. For example,

Example : The RE ab*+b is grouped as ((a(b*))+b) which describes the language

L(a)(L(b))* ÈL(b)

Example : The RE (ab)*+b represents the language È L(b).

Example : It is easy to see that the RE (0+1)*(0+11) represents the language of all

Example : The regular expression r =(00)*(11)*1 denotes the set of all strings with an

.

Solution : Every string in L(r) must contain 00 somewhere, but what comes before and what goes before is completely arbitrary. Considering these observations we can

Example : Considering the above example it becomes clean that the RE (0+1)*11(0+1)*+(0+1)*00(0+1)* represents the set of string over {0,1} that contains the substring 11 or 00.

Example : Consider the RE 0*10*10*. It is not difficult to see that this RE describes the

set of strings over {0,1} that contains exactly two 1's. The presence of two 1's in the

Example : Consider the language of strings over {0,1} containing two or more

Solution : There must be at least two 1's in the RE somewhere and what comes before, between, and after is completely arbitrary. Hence we can write the RE as (0+1)*1(0+1)*1(0+1)*. But following two REs also represent the same language,

i)       0*10*1(0+1)*

ii)      (0+1)*10*10*

Example : Consider a RE r over {0,1} such

Solution : Though it looks similar to ex ……., it is harder to construct to construct. We observer that, whenever a 1 occurs, it must be immediately followed by a 0. This substring may be preceded & followed by any no of 0's. So the final RE must be a repetition of strings of the form: 00…0100….00 i.e. 0*100*. So it looks like the RE is (0*100*)*. But in this case the strings ending in 1 or consisting of all 0's are not

(0*100)(1+Î)+0*(1+Î)

Alternative Solution :

The language can be viewed as repetitions of the strings 0 and 01. Hence get the RE as Î

Regular Expression and Regular Language :

Equivalence(of REs) with FA

Recall that, language that is accepted by some FAs are known as Regular language. The two concepts : REs and Regular language are essentially same i.e. (for) every regular language can be developed by (there is) a RE, and for every RE there is a Regular Langauge. This fact is rather suprising, because RE approach to describing language is fundamentally differnet from the FA approach. But REs and FA are equivalent in their descriptive power. We can put this fact in the focus of the following Theorem.

Theorem : A language is regular iff some RE describes it.

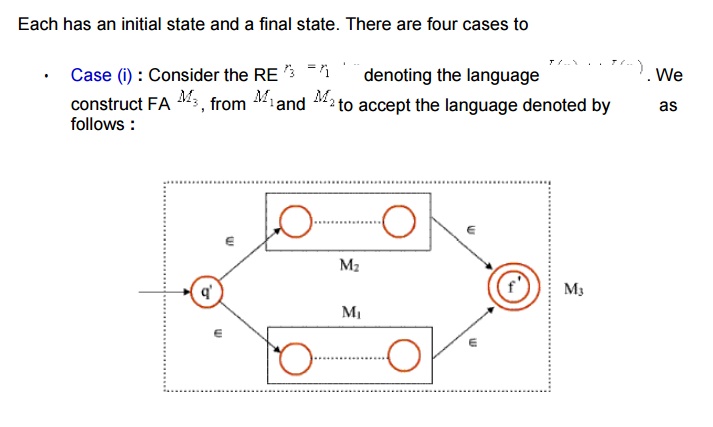
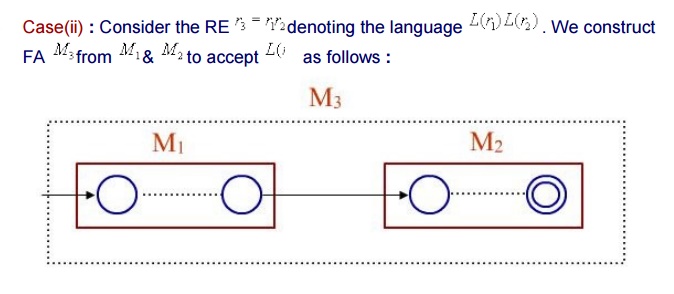
This Theorem has two directions, and are stated & proved below as a separate

RE to FA :

REs denote regular languages :

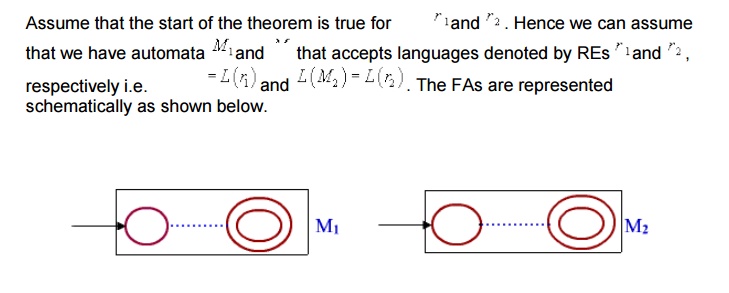
Lemma : If L(r) is a language described by the RE r, then it is regular i.e. there is a FA

 Proof : To prove the lemma, we apply structured index on the expression r. First, show how to construct FA for the basis elements: ϕ,Πand for any aÎå . Then we show how to combine these Finite Automata into Complex Automata that accept the Union, Concatenation, Kleen Closure of the languages accepted by the original Use of NFAs is helpful in the case i.e. we construct NFAs for every REs which are  

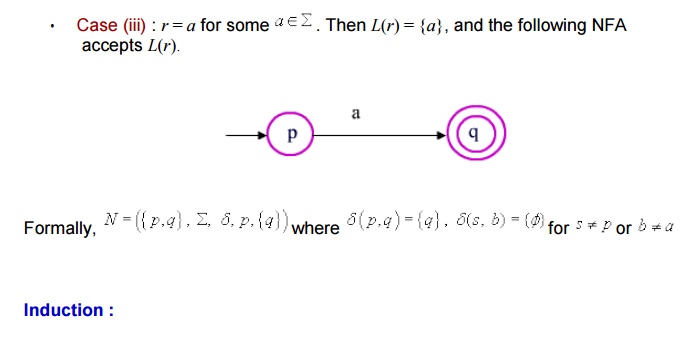
Basis : 

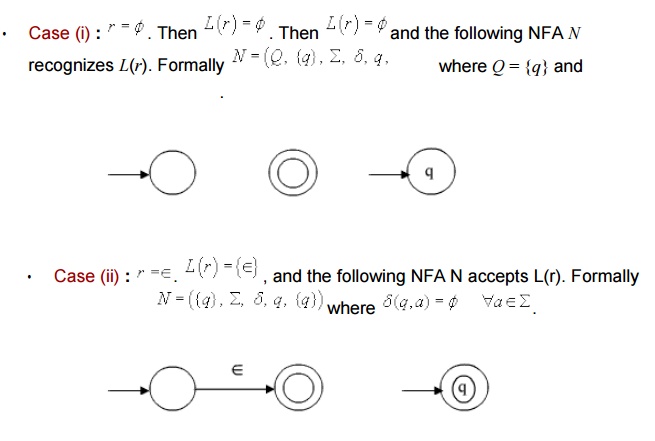
Since the start state is also the accept step, and there is no any transition defined, it  will accept the only string Î and nothing else. 

Non-Deterministic Finite Automata

Nondeterminism is an important abstraction in computer science. Importance of nondeterminism is found in the design of algorithms. For examples, there are many problems with efficient nondeterministic solutions but no known efficient deterministic solutions. ( Travelling salesman, Hamiltonean cycle, clique, etc). Behaviour of a process is in a distributed system is also a good example of nondeterministic situation. Because the behaviour of a process might depend on some messages from other processes that might arrive at arbitrary times with arbitrary contents.

It is easy to construct and comprehend an NFA than DFA for a given regular language. The concept of NFA can also be used in proving many theorems and results. Hence, it plays an important role in this subject.

In the context of FA nondeterminism can be incorporated naturally. That is, an NFA is

•         multiple next state.

•         Î - transitions.

Multiple Next State :

•         In contrast to a DFA, the next state is not necessarily uniquely determined by the current state and input symbol in case of an NFA. (Recall that, in a DFA there is symbol in å ).

Π- transitions :

In an -transition, the tape head doesn't do anything- it doesnot read and it doesnot move. However, the state of the automata can be changed - that is can go to zero, or more states.

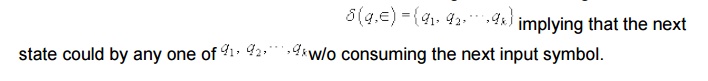
Acceptance :

Informally, an NFA is said to accept its input w  if it is possible to start in some start state and process  w, moving according to the transition rules and making choices along way whenever the next state is not uniquely defined, such that w  is completely processed (i.e. end of  w is reached), the automata is in an accept state. There may several possible paths through the automation in response to an w since the start state is not determined and there are choices along the way because of multiple next automation is said to accept w  if at least one computation path on w starting from at least one start state leads to an accept state- otherwise, the automation  rejects w. Alternatively, we can say that, w is accepted iff there exists a path with w from state. Since there is no mechanism for some start state to some accept state. Since there is no mechanism for which state to start in or which of the possible next moves to take (including w- transitions) in response to an input symbol.

Equivalence of NFA and DFA

It is worth noting that a DFA is a special type of NFA and hence the class of languages accepted by DFA s is a subset of the class of languages accepted by NFA s. Surprisingly, these two classes are in fact equal. NFA s appeared to have more power than DFA s because of generality enjoyed in terms of  -transition and multiple next states. But they are no more powerful than DFA s in terms of the languages they

Converting DFA to NFA

Theorem: Every DFA has as equivalent NFA

Given any NFA we need to construct as equivalent DFA i.e. the DFA need to simulate the behaviour of the NFA . For this, the DFA have to keep track of all the states where the NFA could be in at every step during processing a given input string.

There are 2N possible subsets of states for any NFA with n states. Every subset corresponds to one of the possibilities that the equivalent DFA must keep track of the equivalent DFA will have 2N states.

The formal constructions of an equivalent DFA for any NFA is given below. We first consider an NFA without  transitions and then we incorporate the affects Î transitions later.

Formal construction of an equivalent DFA for a given NFA without Î transitions.

To show that this construction works we need to show that L(D)=L(N)

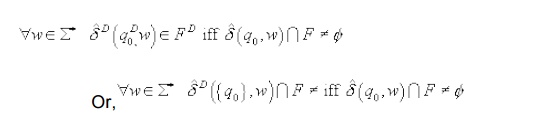
We will prove the following which is a stranger statement thus

Now, given any NFA with Î -transition, we can first construct an equivalent NFA without  Î-transition and then use the above construction process to construct an equivalent

It is also possible to construct an equivalent DFA directly from any given NFA with  Î- transition by integrating the concept  -closure in the above construction.

It is clear that, at every step in the processing of an input string by the DFA D , it enters a state that corresponds to the subset of states that the NFA N could be in at that particular point. This has been proved in the constructions of an equivalent NFA for any If the number of states in the NFA is n , then there are  2N states in the DFA . That is, each state in the DFA is a subset of state of the NFA .

But, it is important to note that most of these 2N  states are inaccessible from the start state and hence can be removed from the DFA without changing the accepted language. Thus, in fact, the number of states in the equivalent DFA would be much than  2N.

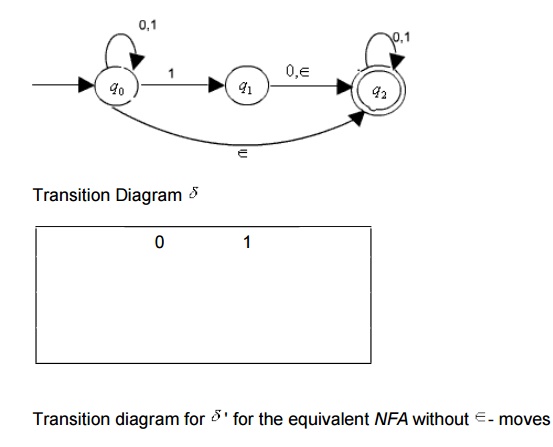
Example : Consider the NFA given below.

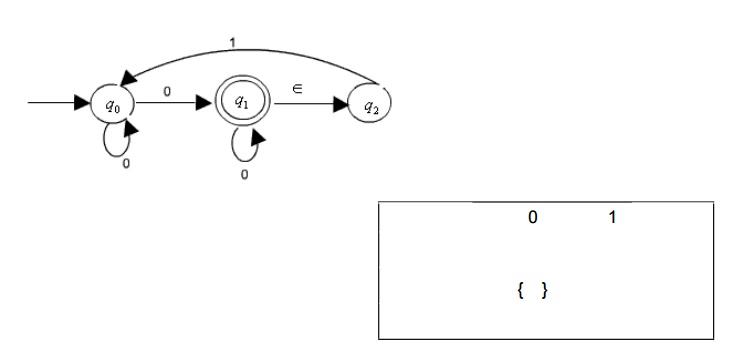
Since there are 3 states in the NFA 

There will be 23=8 states (representing all possible subset of states) in the DFA . The transition table of the DFA constructed by using the subset constructions process is produced here.

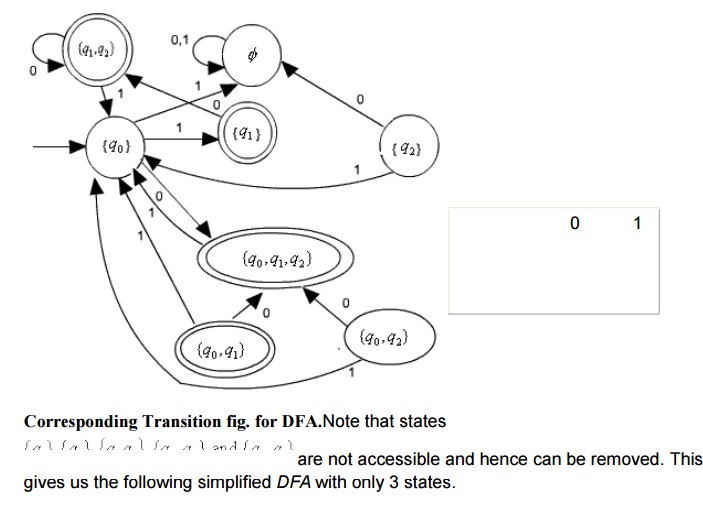
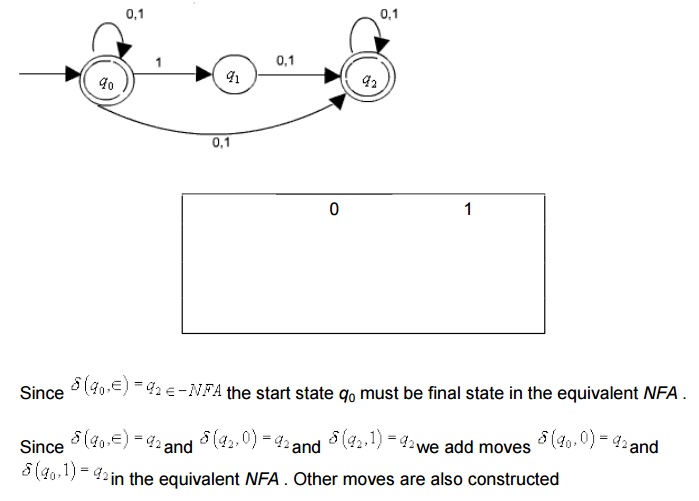
It is interesting to note that we can avoid encountering all those inaccessible or unnecessary states in the equivalent DFA by performing the following two steps