Pushdown Automata

PUSHDOWN AUTOMATA

Grammar

A grammar is a mechanism used for describing languages. This is one of the most simple but yet powerful mechanism. There are other notions to do the same, of course.

In everyday language, like English, we have a set of symbols (alphabet), a set of words constructed from these symbols, and a set of rules using which we can group the words to construct meaningful sentences. The grammar for English tells us what are the words in it and the rules to construct sentences. It also tells us whether a particular sentence is well-formed (as per the grammar) or not. But even if one follows the rules of the english grammar it may lead to some sentences which are not meaningful at all, because of impreciseness and ambiguities involved in the language. In english grammar we use many other higher level

< sentence >  -- > < noun-phrase > < predicate >

meaning that "a sentence can be constructed using a 'noun-phrase' followed by a predicate".

Some more rules are as follows:

< noun-phrase >   -- >  < article >< noun >

< predicate >   -- >  < verb >

with similar kind of interpretation given above.

If we take {a, an, the} to be <article>; cow, bird, boy, Ram, pen to be examples of <noun>; and eats, runs, swims, walks, are associated with <verb>, then we can construct the sentence- a cow runs, the boy eats, an pen walks- using the above rules. Even though all sentences are well-formed, the last one is not meaningful. We observe that we start with the higher level construct <sentence> and then reduce it to <noun-phrase>,

<article>, <noun>, <verb> successively, eventually leading to a group of words associated with these

These concepts are generalized in formal language leading to formal grammars. The word 'formal' here refers to the fact that the specified rules for the language are explicitly stated in terms of what strings or symbols can occur. There can be no ambiguity in it.

Formal definitions of a Grammar

Successive strings are dervied by applying the productions rules of the grammar in any arbitrary order.

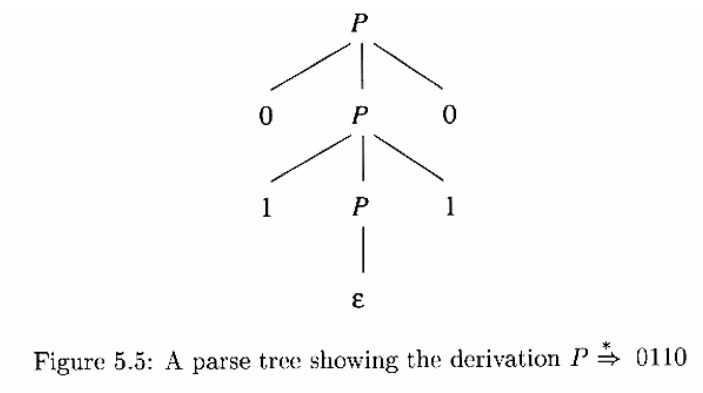
By applying the production rules in arbitrary order, any given grammar can generate many strings of terminal symbols starting with the special start symbol, S, of the grammar. 

By using the first production, it generates the string ab ( for i =1 ).

Push down automata:

Regular language can be charaterized as the language accepted by finite automata. Similarly, we can characterize the context-free language as the langauge accepted by a class of machines called "Pushdown A uto mata" (PDA). A pushdown automation is an extension of the NFA.

It is observed that FA have limited capability. (in the sense that the class of languages accepted or characterized by them is small). This is due to the "f in i te me mo ry" (number of states) and "no ex te rnal involved with them. A PDA is simply an NFA augmented with an "ex te r nal s tack me mory". The addition of a stack provides the PDA with a last-in, first-out memory management cpapability. This "S tack" or "pushdown store" can be used to record a potentially unbounded information. It is due to this memory management accept many interesting languages like  {a^xb^x|n>=0}. Although, a PDA can store an unbounded amount of information on the stack, its access to the information on the stack is limited. It can push an element onto the top of the stack and pop off an element from the top of the stack. To read down into the stack the top elements must be popped off and are lost. Due to this limited access to the information on the stack, a PDA still has some limitations and cannot accept some other interesting languages.

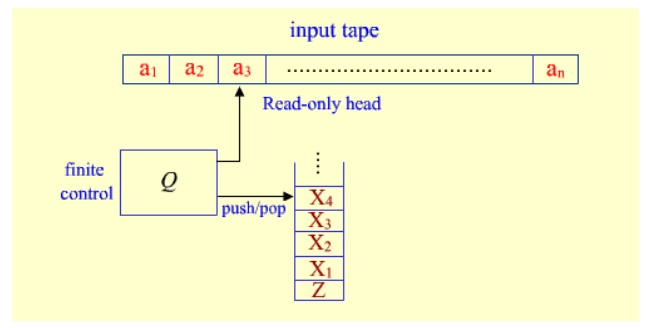
As shown in figure, a PDA has three components: an input tape with read only head, a finite control and a pushdown store.

The input head is read-only and may only move from left to right, one symbol (or cell) at a time. In each step, the PDA pops the top symbol off the stack; based on this symbol, the input symbol it is currently reading, its present state, it can push a sequence of symbols onto the stack, move its read-only head one cell (or symbol) to the right, and enter a new state, as defined by the transition rules of the PDA.

PDA are nondeterministic, by default. That is, Î - transitions are also allowed in which the PDA can pop and push, and change state without reading the next input symbol or moving its read-only head. Besides this, there may be multiple options for possible next moves.

Formal Definitions : Formally, a PDA M is a 7-tuple M

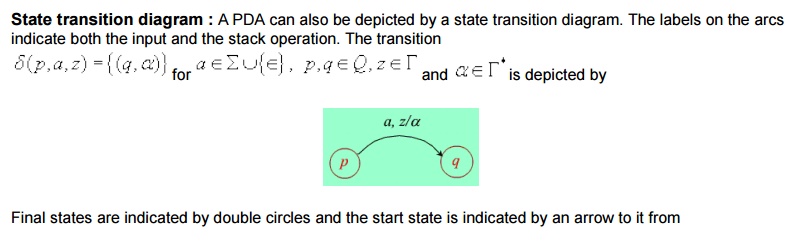
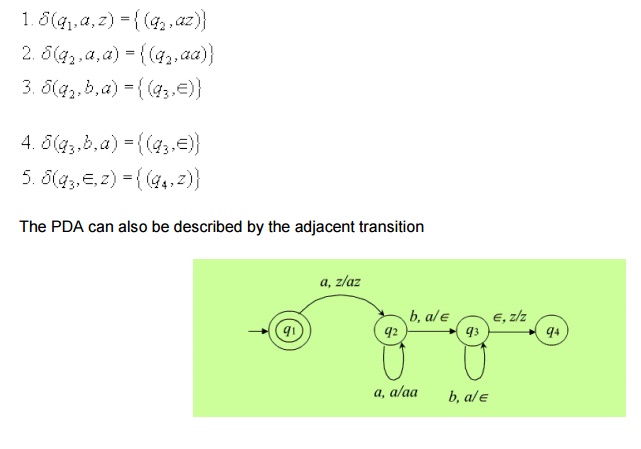
Informally, whenever the PDA M sees an input a in the start q₁ with the start symbol z on the top of the stack it pushes a onto the stack and changes state to  q₂. (to remember that it has seen the first 'a'). On state  if it sees anymore a, q₂ it simply pushes it onto the stack. Note that when M is on state q₂ , the symbol on the top of the stack can only be a. On state q₂  if it sees the first b with a on the top of the stack, then it needs to start comparison of numbers of a's and b's, since all the a's at the begining of the input have already been pushed onto the stack. It start this process by popping off the a from the top of the stack and enters in state q3 (to remember that the comparison process has begun). On q₃ , it expects only b's in the input (if it sees any more a in the input thus the input will not be in the proper form of anbn). Hence there is no more on input when it is in state q₃ . On state q₃ it pops off an a from the top of the stack for every b in the input. When sees the last b on state q3 (i.e. when the input is exaushted), then the last a from the stack will be popped off and the start symbol z is exposed. This is the only possible case when the input (i.e. Î -input ) the PDA will move to state q₄ which is an accept state.

we can show the computation of the PDA on a given input using the IDs and next move relations. For example,

Let the input be aabb. we start with the start configuration and proceed to the subsequent IDs using the transition function defined

we can show the computation of the PDA on a given input using the IDs and next move relations. For example,

i) Let the input be aabab.

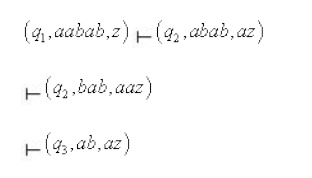
No further move is defined at this point.

Hence the PDA gets stuck and the string aabab is not accepted.

Example 2 : We give an example of a PDA M that accepts the set of balanced strings of parentheses [] by empty stack.

The PDA M is given below.

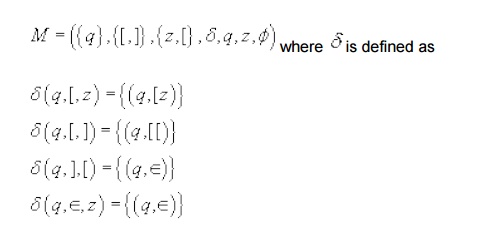
Informally, whenever it sees a [, it will push the ] onto the stack. (first two transitions), and whenever it sees a ] and the top of the stack symbol is [, it will pop the symbol [ off the stack. (The third transition). The fourth transition is used when the input is exhausted in order to pop z off the stack ( to empty the stack) and accept. Note that there is only one state and no final state. The following is a sequence of configurations leading to the acceptance of the string [ [ ] [ ] ] [ ].

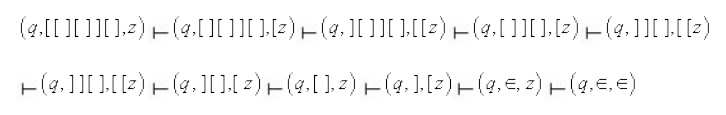
Equivalence of acceptance by final state and empty

It turns out that the two definitions of acceptance of a language by a PDA - accpetance by final state and empty stack- are equivalent in the sense that if a language can be accepted by empty stack by some PDA, it can also be accepted by final state by some other PDA and vice versa. Hence it doesn't matter which one we use, since each kind of machine can simulate the other.Given any arbitrary PDA M that accpets the language L by final state or empty stack, we can always construct an equivalent PDA M with a single final state that accpets exactly the same language L. The construction process of M' from M and the proof of equivalence of M & M' are given below.

There are two cases to be considered.

Transitions 1 causes M’ to enter the initial configuration of M except that M’ will have its own bottom-of-stack marker X which is below the symbols of M's stack. From this point onward M’ will simulate every move of M since all the transitions of M are also in  M’

If M ever empties its stack, then M’ when simulating M will empty its stack except the symbol X  At this point, M’ will enter its final state  by using transition rule 2, thereby (correctly) accepting the input. We will prove that M and M’ are equivalent.

Hence, M starting with its initial configuration will eventually empty its stack and accept the input

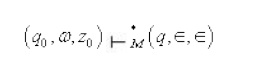
Equivalence of PDA’s and CFG’s:

We will now show that pushdown automata and context-free grammars are equivalent in expressive power, that is, the language accepted by PDAs are exactly the context-free languages. To show this, we have to prove each of the following:

i)       Given any arbitrary CFG G there exists some PDA M that accepts exactly the same language generated by G.

ii)      Given any arbitrary PDA M there exists a CFG G that generates exactly the same language accpeted by M.

(i) CFA to PDA

We will first prove that the first part i.e. we want to show to convert a given CFG to an equivalent

The one state PDA M equivalent to G is shown below. For convenience, a production of G and the corresponding transition in M are marked by the same encircled number.

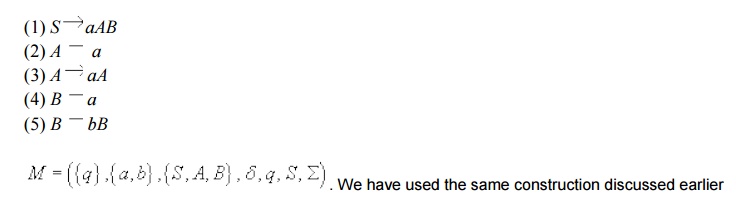
Some Useful Explanations :

Consider the moves of M on input aaaba leading to acceptance of the string.

Steps

Note : encircled numbers here shows the transitions rule applied at every step.

Now consider the derivation of the same string under grammar G. Once again, the production used at every step is shown with encircled number.

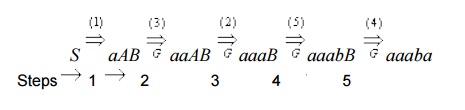
Observations:

•        There is an one-to-one correspondence of the sequence of moves of the PDA M and the derivation sequence under the CFG G for the same input string in the sense that - number of steps in both the cases are same and transition rule corresponding to the same production is used at every step (as shown by encircled number).

•        considering the moves of the PDA and derivation under G together, it is also observed that at every step the input read so far and the stack content together is exactly identical to the corresponding sentential form i.e.

<what is Read><stack> = <sentential form>

Say, at step 2, Read so far = a

Thus N(M) = L(G) as desired. Note that we have already proved a more general version of the claim PDA and CFG:

We now want to show that for every PDA M that accpets by empty stack, there is a CFG G such that L(G)

=

we first see whether the "reverse of the construction" that was used in part (i) can be used here to construct an

It can be show that this reverse construction works only for single state

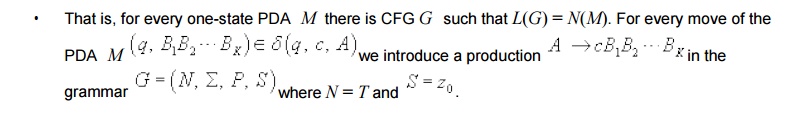
we can now apply the proof in part (i) in the reverse direction to show that L(G) = N(M).

But the reverse construction does not work for PDAs with more than one state. For example, consider the M produced here to accept the language

We can drive strings like aabaa which is in the language. 

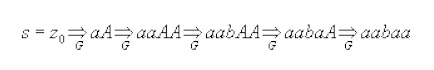
But under this grammar we can also derive some strings which are not in the language.

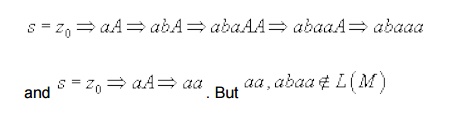
Therefore, to complete the proof of part (ii) we need to prove the following claim

It is quite possible to prove the above claim. But here we will adopt a different approach. We start with any

PDA to CFG

We want to construct a CFG G to simulate any arbitrary PDA M with one or more states. Without loss of generality we can assume that the PDA M accepts by empty stack.

The idea is to use nonterminal of the form <PAq> whenever PDA M in state P with A on top of the stack goes to state q₀ . That is, for example, for a given transition of the PDA corresponding production in the grammar shown below,

Include the follwoing production 

if PDA M accepts w by empty stack or L(G) = N(M) 

Now, to show that the above construction of CFG G from any PDA M works, we need to prove the proposed claim.

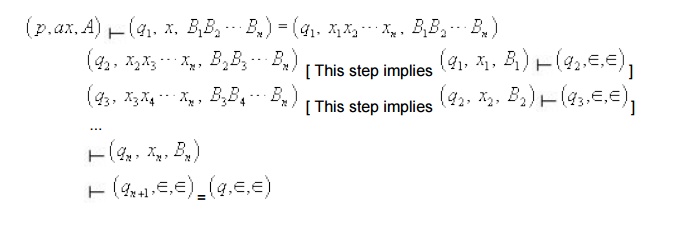
[ Note: Each step takes less than or equal to n -1 moves because the total number of moves required assumed

That is, in general

in M we have added the following production in G.

We can show the computation of the PDA on a given input using the IDs and next move relations. For example,

following are the computation on two input strings.

i) Let the input be aabb. we start with the start configuration and proceed to the subsequent IDs using the

So the string aabb is rightly accepted by M.

we can show the computation of the PDA on a given input using the IDs and next move relations. For example,

i) Let the input be aabab.

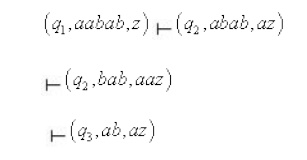
No further move is defined at this point.

Hence the PDA gets stuck and the string aabab is not accepted.

The following is a sequence of configurations leading to the acceptance of the string [ [ ] [ ] ] [

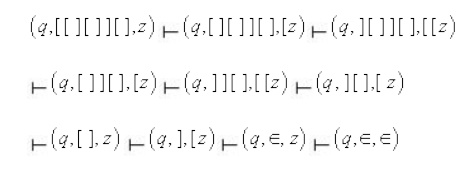
Equivalence of acceptance by final state and empty

It turns out that the two definitions of acceptance of a language by a PDA - accpetance by final state and empty stack- are equivalent in the sense that if a language can be accepted by empty stack by some PDA, it can also be accepted by final state by some other PDA and vice versa. Hence it doesn't matter which one we use, since each kind of machine can simulate the other.Given any arbitrary PDA M that accpets the language L by final state or empty stack, we can always construct an equivalent PDA M with a single final state that accpets exactly the same language L. The construction process of M' from M and the proof of equivalence of M & M'

There are two cases to be considered.

Equivalence of acceptance by final state and empty

It turns out that the two definitions of acceptance of a language by a PDA - accpetance by final state and empty stack- are equivalent in the sense that if a language can be accepted by empty stack by some PDA, it can also be accepted by final state by some other PDA and vice versa. Hence it doesn't matter which one we use, since each kind of machine can simulate the other.Given any arbitrary PDA M that accpets the language L by final  state or empty stack, we can always construct an equivalent PDA M with a single final state that accpets  exactly the same language L. The construction process of M' from M and the proof of equivalence of M & M' 

There are two cases to be considered.

CASE 2 : PDA M accepts by empty

Regular Languages and DPDA’s The DPDA’s accepts a class of languages that is in between the regular languages and CFL’s.

Deterministic Pushdown Automata (DPDA) and Deterministic Context-free Languages

Pushdown automata that we have already defined and discussed are nondeterministic by default, that is , there may be two more moves involving the same combinations of state, input symbol, and top of the stock, and again, for some state top of the stock the machine may either read and input symbol or make an Î - transition (without consuming any input).

In deterministic PDA , there is never a choice of move in any situation. This is handled by preventing the above mentioned two cases as described in the definition below.

 (This condition prevents the possibility of a choice between a move with or without an input)