Chapter: Theory of Computation
Grammars - Regular Expressions and Languages
GRAMMARS
Regular
Expressions: Formal
We construct REs from primitive constituents
(basic elements) by repeatedly applying certain recursive rules as given below.
(In the definition)
Definition
: Let S be an alphabet. The regular
expressions are defined recursively as
Basis :
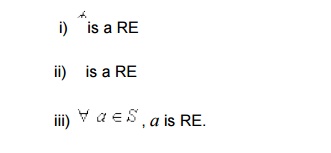
These are called primitive regular expression
i.e. Primitive
Recursive
Step :

Closure : r is RE over only if it can be
obtained from the basis elements (Primitive REs) by a finite no of applications
of the recursive step (given in 2).
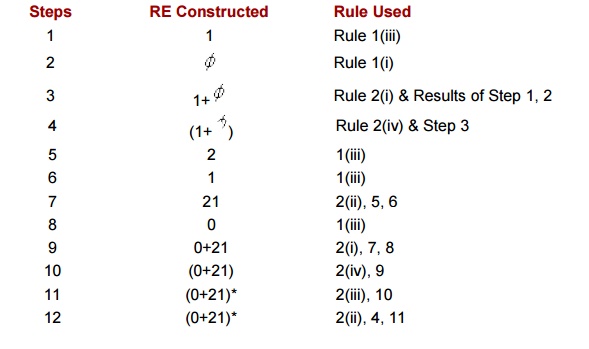
Example : Let
å = { 0,1,2 }. Then (0+21)*(1+ F ) is a RE, because we can construct this
expression applying the above rules as given in the following step.
Language
described by REs : Each describes a language (or a language is
associated with every RE).
Notation
: If r is a
RE over some alphabet then L(r) is the language associate with r . We can
define the

Example : Consider the RE (0*(0+1)). Thus the language denoted by the RE is

Precedence
Rule
Consider the RE ab + c. The language described by the RE can be thought of either L(a)L(b+c) or L(ab)È L( c) as provided by the rules (of languages described by REs) given already. But these represents two different languages lending to ambiguity. To remove this ambiguity we can either
1) Use
fully parenthesized expression- (cumbersome) or
2) Use
a set of precedence rules to evaluate the options of REs in some order. Like
other algebras mod in mathematics.
For REs, the order of precedence for the
operators is as follows:
i) The
star operator precedes concatenation and concatenation precedes union (+)
operator.
ii) It
is also important to note that concatenation & union (+) operators are
associative and union operation is commutative.
Using these precedence rule, we find that the RE
ab+c represents the language L(ab) È L(c) i.e. it should be grouped as ((ab)+c).
We can, of course change the order of precedence
by using parentheses. For example, the language represented by the RE a(b+c) is
L(a)L(b+c).
Example
: The RE ab*+b is grouped as ((a(b*))+b) which
describes the language L(a)(L(b))* ÈL(b)
Example
: The RE (ab)*+b represents the language
(L(a)L(b))* È L(b).
Example
: It is easy to see that the RE (0+1)*(0+11)
represents the language of all strings over {0,1} which are either ended with 0
or 11.
Example
: The regular expression r =(00)*(11)*1 denotes the set of all strings with an even number
of 0's followed by an odd number of 1's i.e.
Note
: The notation
r+ is used to
represent the RE rr*. Similarly, r2 represents the RE rr,r3 denotes r2r, and so on.
An arbitrary string over å = {0,1} is denoted as (0+1)*.
Exercise
: Give a RE r over {0,1} s.t.
L(r)= 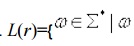
has at least one pair of consecutive 1's}
Solution
: Every string in L(r) must contain 00 somewhere,
but what comes before and what goes before is completely arbitrary. Considering
these observations we can write the REs as (0+1)*11(0+1)*.
Example
: Considering the above example it becomes clean
that the RE (0+1)*11(0+1)*+(0+1)*00(0+1)* represents the set of string over
{0,1} that contains the substring 11 or 00.
Example
: Consider the RE 0*10*10*. It is not difficult to
see that this RE describes the set of strings over {0,1} that contains exactly
two 1's. The presence of two 1's in the RE and any no of 0's before, between
and after .
Example : Consider the language of strings over
{0,1} containing two or more
Solution
: There must be at least two 1's in the RE
somewhere and what comes before, between, and after is completely arbitrary.
Hence we can write the RE as (0+1)*1(0+1)*1(0+1)*. But following two REs also
represent the same language, each ensuring presence of least two 1's somewhere
in the string
i) 0*10*1(0+1)*
ii) (0+1)*10*10*
Example
: Consider a RE r over {0,1} such that
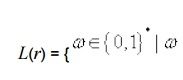
has no pair of consecutive 1's}
Solution
: Though it looks similar to ex ……., it is harder
to construct to construct. We observer that, whenever
a 1 occurs, it must be immediately followed by a
0. This substring may be preceded & followed by any no of 0's. So the final
RE must be a repetition of strings of the form: 00…0100….00 i.e. 0*100*. So it
looks like the these observations into consideration, the final RE is r =
(0*100*)(1+ Î )+0*(1+ Î).
Alternative
Solution :
The language can be viewed as repetitions of the
strings 0 and 01. Hence get the RE as r = (0+10)*(1+ Î).This is a shorter expression but represents
the same language.
Regular Expression:
FA to regular expressions:
FA
to RE (REs for Regular Languages)
Lemma: If a language is regular, then there is a RE to
describe it. i.e. if L = L(M) for some DFA M, then there is a RE r such that L
= L(r).
Proof
: We need to construct a RE r such L(r)={w|wÎL(M)}. Since M is a DFA, it has a finite no of
states. Let the set of states of M is Q = {1, 2, 3,..., n} for some integer n.
[ Note : if the n states of M were denoted by some other symbols, we can always
rename those to indicate as 1, 2, 3,..., n ].
Notations
: rij(k) is a RE denoting
the language which is the set of all strings w such that w is the label of path
from state i to state (1<=I,j<=n)
in M, and that path has no intermediate state whose number is greater
then k. ( i & j (begining and end pts) are not considered to be
"intermediate" so i and /or j can be greater than k )


Induction
:
Assume that there exists a path from state i to
state j such that there is no intermediate state whose number greater than k.
The corresponding Re for the label of the path is rij(k). There are only
two possible cases :
1. The
path dose not go through the state k at all i.e. number of all the intermediate
states are less than k. So, the label of the path from state i to state j is
tha language described by the rij(k-1).
2. The
path goes through the state k at least once. The path may go from i to j and k
may appear more than once. We can break the into pieces as shown in the figure
7.
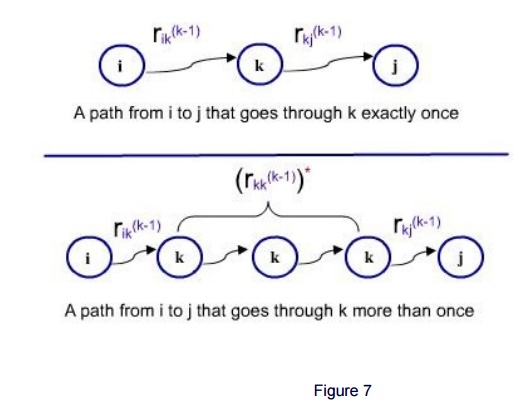
1. The first part from the state i to the state
k which is the first recurence. In this path, all intermediate states are less
than k and it starts at iand ends at k. So the RE rik(k-1)
denotes the language of the label of path.
2. The last part from the last occurence of the
state k in the path to state j. In this path also, no intermediate state is
numbered greater than k. Hence the RE rkj(k-1)
denoting the language of the label of the path.
3. In the middle, for the first occurence of k
to the last occurence of k , represents a loop which may be taken zero times,
once or any no of times. And all states between two consecutive k's are
numbered less than k.
Hence the label of the path of the part is
denoted by the RE rij(k-1)*. The label of the path from
state i to state j is the concatenation of these 3 parts which is
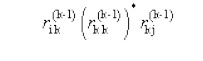
Since either case 1 or case 2 may happen the
labels of all paths from state i to j is denoted by the following

Since rij1(n)
is the set of all strings that starts at start state 1 and finishes at final following the transition of the FA with
any value of the intermediate state (1, 2, ... , n) and hence accepted by the
automata.
Regular Grammar:

A right or left-linear grammar is called a
regular grammar.
Regular grammar and Finite Automata are
equivalent as stated in the following
Theorem : A language L is
regular iff it has a regular grammar. We use the following two lemmas to prove the
above theorem.
Lemma 1 : If L is
a regular language, then L is
generated by some right-linear

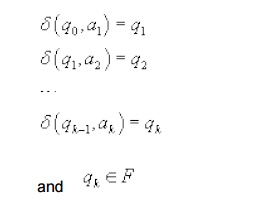
By construction, the grammar G will have one
production for each of the above transitions. Therefore, we have the
corresponding derivation.
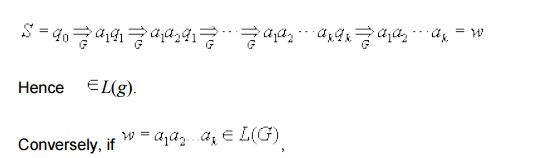
then the derivation of w in G must have the form
as given above. But, then
the construction of G from M implies that

We now show that this construction works.


It is easy to see that G generates the language
denoted by the regular expression (01)*0.
The construction of lemma 2 for this grammar
produces the follwoing FA. This FA accepts exactly (01)*1.
Decisions Algorithms for CFL
In this section, we examine some questions about
CFLs we can answer. A CFL may be represented using a CFG or PDA. But an
algorithm that uses one representation can be made to work for the others,
since we can construct one from the other.
Testing
Emptiness :
Theorem : There are algorithms to test
emptiness

Let us first present a simple but inefficient algorithm.

Pumping Lemma:
Limitations of Finite Automata and Non regular Languages
The class of languages recognized by FA s is
strictly the regular set. There are certain languages which are non regular
i.e. cannot be recognized by any FA
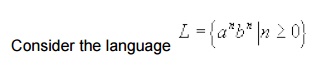
In order to accept is language, we find that, an
automaton seems to need to remember when passing the center point between a's
and b's how many a's it has seen so far. Because it would have to compare that
with the number of b's to either accept (when the two numbers are same) or
reject (when they are not same) the But the number of a's is not limited and
may be much larger than the number of states since the string may be
arbitrarily long. So, the amount of information the automaton need to remember
is unbounded.
A finite automaton cannot remember this with
only finite memory (i.e. finite number of states). The fact that FA s have
finite memory imposes some limitations on the structure of the languages
recognized. Inductively, we can say that a language is regular only if in
processing any string in this language, the information that has to be
remembered at any point is strictly limited. The argument given above to show
that is non regular is informal. We now
present a formal method for showing that anbn certain
languages such anbn are non regular
Properties
of CFL’s
Closure
properties of CFL:
We consider some important closure properties of
CFLs.




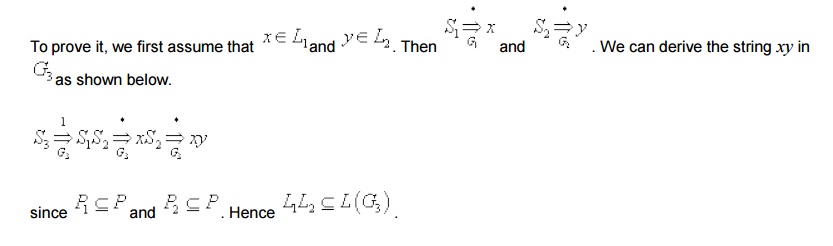











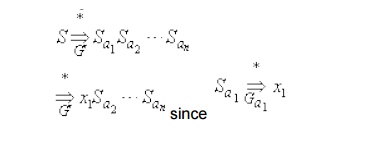

Related Topics