Unit Commitment Solution Methods

UNIT COMMITMENT SOLUTION METHODS

The commitment problem can be very difficult. As a theoretical exercise, let us postulate the following situation.

1.        We must establish a loading pattern for M periods.

2.        We have N units to commit and dispatch.

3.        The M load levels and operating limits on the N units are such that any one unit can supply the individual loads and that any combination of units can also supply the loads.

Next, assume we are going to establish the commitment by enumeration (brute force). The total number of combinations we need to try each hour is,

C (N, 1) + C (N,2) + ... + C(N, N - 1) + C ( N , N ) = 2N – 1-----------------------------------(18)

Where C (N, j) is the combination of N items taken j at a time. That is,

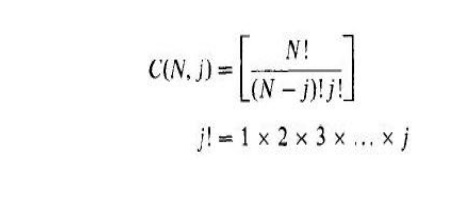
For the total period of M intervals, the maximum number of possible combinations is (2N - l)M, which can become a horrid number to think about.

For example, take a 24-h period (e.g., 24 one-hour intervals) and consider systems with 5, 10, 20 and 40 units.

Ø   These very large numbers are the upper bounds for the number of enumerations required.

Ø   Fortunately, the constraints on the units and the load-capacity relationships of typical  utility systems  are such that  we do  not  approach these large numbers.

Ø   Nevertheless, the real practical barrier in the optimized unit commitment problem is the high dimensionality of the possible solution space.

Ø   The most talked-about techniques for the solution of the unit commitment problem are:

1.   Priority-list schemes,

2.   Dynamic programming (DP),

3.   Lagrange relation (LR).

1. Priority-List Method

Ø   The simplest unit commitment solution method consists of creating a priority list of units.

Ø   A simple shut-down rule or priority-list scheme could be obtained after an exhaustive enumeration of all unit combinations at each load level.

Ø   The priority list could be obtained in a much simpler manner by noting the full- load average production cost of each unit, where the full-load average production cost is simply the net heat rate at full load multiplied by the fuel cost.

Priority List Method:

Priority list method is the simplest unit commitment solution which consists of creating a priority list of units.

Full load average production cos t= Net heat rate at full load X Fuel cost

Assumptions:

1. No load cost is zero

2. Unit input-output characteristics are linear between zero output  and full load

3. Start up costs are a fixed amount

4. Ignore  minimum  up  time  and  minimum  down time Steps to be followed

1. Determine the full load average production cost for each units

2. Form priority order based on average production cost

3. Commit number of units corresponding to the priority order

4.   Alculate PG1, PG2 ………….PGN from economic dispatch problem for the feasible combinations only.

5. For the load curve shown.

Assume load is dropping or decreasing, determine whether dropping the next unit will supply generation & spinning reserve.

If not, continue as it is

If yes, go to the next step

6. Determine the number of hours H, before the unit will be needed again.

7. Check H< minimum shut down time.

If not, go to the last step  If yes, go to the next step

8. Calculate two costs

1. Sumof hourly production for the next H hours with the unit up

2. Recalculate the same for the unit down + start up cost for either cooling or banking

9. Repeat  the  procedure  until  the  priority

list Merits:

1. No need to go for N combinations

2. Take only one constraint

3. Ignore the minimum up time & down time

4. Complication reduced

Demerits:

1. Start up cost are fixed amount

2. No load costs are not considered.

2. Dynamic-Programming Solution

Dynamic programming has many advantages over the enumeration scheme, the chief advantage being a reduction in the dimensionality of the problem. Suppose we have found units in a system and any combination of them could serve the (single) load. There would be a maximum of 24 - 1 = 15 combinations to test. However, if a strict priority order is imposed, there are only four combinations to try:

Priority 1 unit

Priority 1 unit + Priority 2 unit

Priority 1 unit + Priority 2 unit + Priority 3 unit

Priority 1 unit + Priority 2 unit + Priority 3 unit + Priority 4 unit

The imposition of a priority list arranged in order of the full-load averagecost rate would 

result in a theoretically correct dispatch and commitment only if:

1. No load costs are zero.

2. Unit input-output characteristics are linear between zero output and full load.

3. There are no other restrictions.

4. Start-up costs are a fixed amount.

In the dynamic-programming approach that follows, we assume that:

1. A state consists of an array of units with specified units operating and

2. The start-up cost of a unit is independent of the time it has been off-line

3. There are no costs for shutting down a unit.

4.  There is a strict priority order, and in each interval a specified minimum the rest off-line. (i.e., it is a fixed amount).amount of capacity must be operating.

A feasible state is one in which the committed units can supply the required load and that meets the minimum amount of capacity each period.

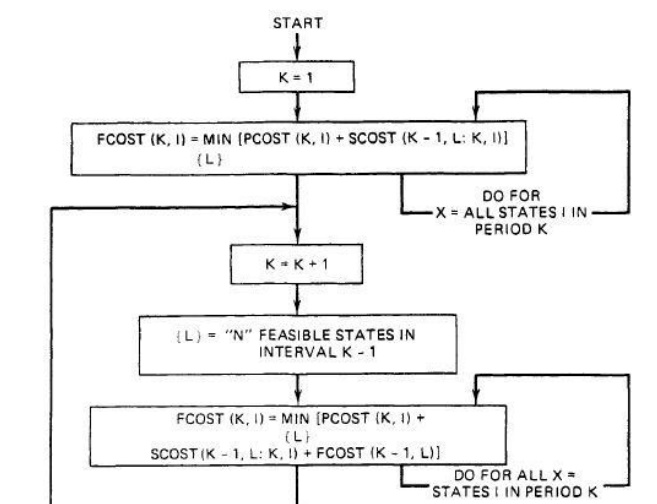
3. Forward DP Approach

Ø   One could set up a dynamic-programming algorithm to run backward in time starting from the final hour to be studied, back to the initial hour.

Ø   Conversely, one could set up the algorithm to run forward in time from the initial hour to the final hour.

Ø   The forward approach has distinct advantages in solving generator unit commitment. For example, if the start-up cost of a unit is a function of the time it has been off-line (i.e., its temperature), then a forward dynamic-program approach is more suitable since the previous history of the unit can be computed at each stage.

Ø   There are other practical reasons for going forward.

Ø   The initial conditions are easily specified and the computations can go forward in time as long as required.

Ø   A forward dynamic-programming algorithm is shown by the flowchart

The recursive algorithm to compute the minimum cost in hour K with combination

Where

Fcost(K, I ) = least total cost to arrive at state ( K , I ) Pcost(KI, ) = production cost for state ( K ,I )

Scost(K - 1, L: K , I)= transition cost from state (K - 1, L) to state ( K , I )

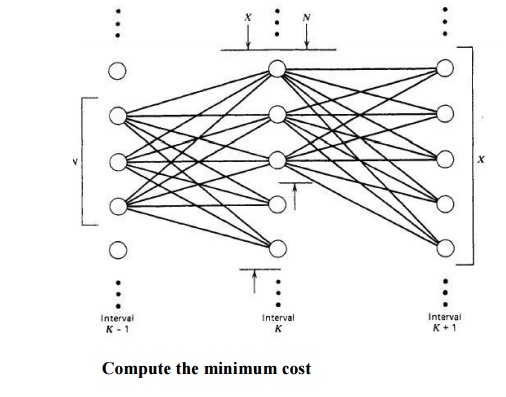
State (K, 1) is the Zth combination in hour K. For the forward dynamic programming approach, we define a strategy as the transition, or path, from one state at a given hour to a state at the next hour.

Note that two new variables, X and N, have been introduced in Figure. X = number of states to search each period

N = number of strategies, or paths, to save at each step

These variables allow control of the computational effort (see below Figure).For complete enumeration, the maximum number of the value of X or Nis 2n – 1