Chapter: Power System Operation and Control : Commitment and Economic Dispatch

Base Point and Participation Factors

This method assumes that the economic dispatch problem has to be solved repeatedly by moving the generators from one economically optimum schedule to another as the load changes by a reasonably small amount.

BASE POINT AND PARTICIPATION FACTORS

^ØThis method assumes that the economic dispatch problem has to be solved repeatedly by moving the generators from one economically optimum schedule to another as the load changes by a reasonably small amount.

^ØWe start from a given schedule-the base point.

Next, the scheduler assumes a load change and investigates how much each generating unit needs to be moved (i.e.,“participate” in the load change) in order that the new load be served at the most economic operating point.

^ØAssume that both the first and second derivatives in the cost versus power output function are available (Le., both F; and Fy exist). The incremental cost curve of i^th unit given in the fig.

^ØAs the unit load is changed by an amount, the

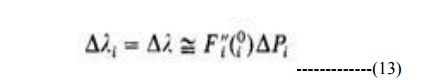
(13) This is true for each of the N units on the system, so that

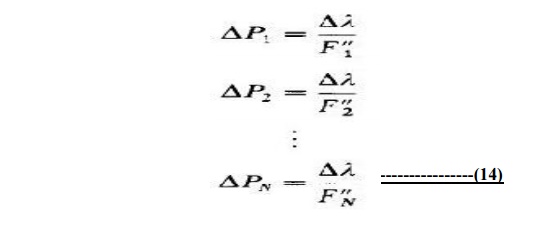
The total change in generation (=change in total system demand) is, of course, the sum of the individual unit changes. Let P_d be the total demand on the generators (where P_load+P_loss&), then

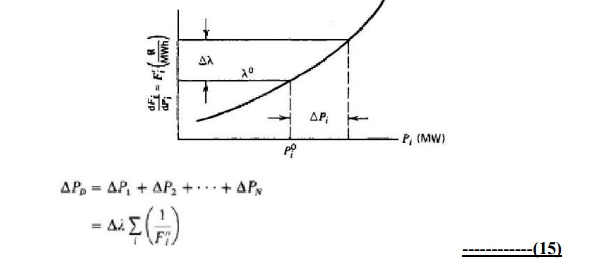
The earlier equation, 15, can be used to find the participation factor for each unit as follows

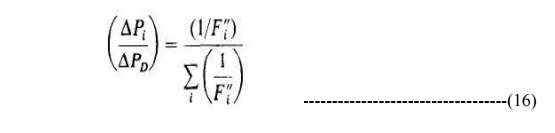
^ØThe computer implementation of such a scheme of economic dispatch is straightforward.

^ØIt might be done by provision of tables of the values of FY as a function of the load levels and devising a simple scheme to take the existing load plus the projected increase to look up these data and compute the factors.

^ØSomewhat less elegant scheme to provide participation factors would involve a repeat economic dispatch calculation at.

^ØThe base-point economic generation values are then subtracted from the new economic generation values and the difference divided to provide the participation factors.

^ØThis scheme works well in computer implementations where the execution time for the economic dispatch is short and will always give consistent answers when units reach limits, pass through break points on piecewise linear incremental cost functions, or have non convex cost curves.

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

Power System Operation and Control : Commitment and Economic Dispatch : Base Point and Participation Factors |