Economic Dispatch Without Loss

ECONOMIC DISPATCH WITHOUT LOSS

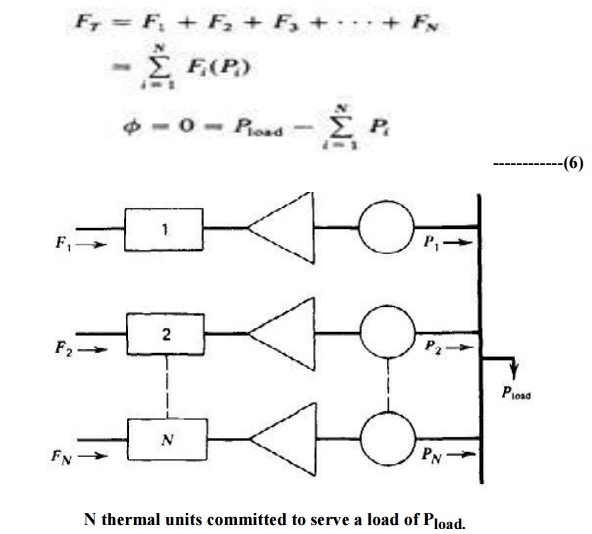
^Ø    This system consists of N thermal-generating units connected to a single bus-bar serving a received electrical load P_load input to each unit, shown as F_I,represents the cost rate of the unit.

Ø  The output of each unit, P_i, is the electrical power generated by that particular unit. The total cost rate of this system is, of course, the sum of the costs of each of the individual units.

^Ø    The essential constraint on the operation of this system is that the sum of the output powers must equal the load demand.

^Ø    Mathematically speaking, the problem may be stated  very concisely.

^Ø That is, an objective function, F_T, is equal to the total cost for supplying the indicated load.

^Ø    The problem is to minimize F_T subject to the constraint that the sum of the powers generated must equal the received load.

^Ø    Note that any transmission losses are neglected and any operating limits are not explicitly stated when formulating this problem. That is,

^Ø   This is a constrained optimization problem that may be attacked formally using advanced calculus methods that involve the Lagrange function.

^Ø   In order to establish the necessary conditions for an extreme value of the objective function, add the constraint function to the objective function after the constraint function has been multiplied by an undetermined multiplier.

^Ø    This is known as the Lagrange function and is shown in Eq(7)

^Ø   The necessary conditions for an extreme value of the objective function result when we take the first derivative of the Lagrange function with respect to each of the independent variables and set the derivatives equal to zero. In this case,there are N+1 variables, the N

^Ø   values of power output, P_i, plus the undetermined Lagrange multiplier, λ.

^Ø   The derivative of the Lagrange function with respect to the undetermined multiplier merely gives back the constraint equation.

^Ø   On the other hand, the N equations that result when we take the partial derivative of the Lagrange function with respect to the power output values one at a time give the set of equations shown as Eq. 8.

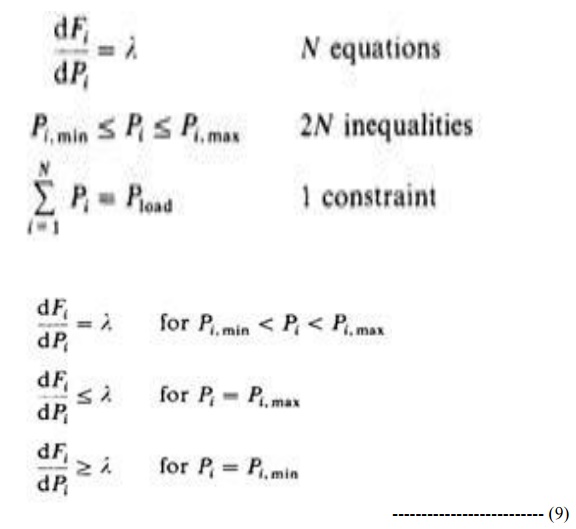
When we recognize the inequality constraints, then the necessary conditions may be expanded slightly as shown in the set of equations making up Eq. 9.