Economic Dispatch Solution By Lambda-Iteration Method

ECONOMIC DISPATCH SOLUTION BY LAMBDA-ITERATION METHOD

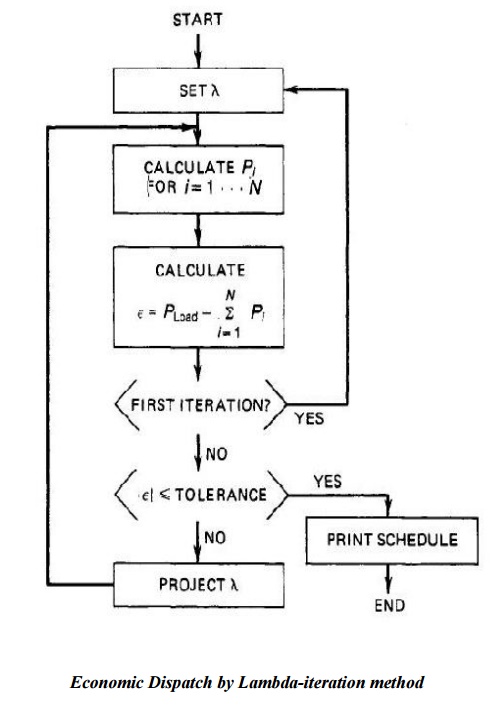
^Ø   Block diagram of the lambda-iteration method of solution for the all-thermal, dispatching problem-neglecting losses.

^Ø   We can approach the solution to this problem by considering a graphical technique for solving the problem and then extending this into the area of computer algorithms.

^Ø   Suppose we have a three-machine system and wish to find the optimum economic operating point.

One approach would be to plot the incremental cost characteristics for each of these three units on the same graph, In order to establish the operating points of each of these three units such that we have minimum cost and at the same time satisfy the specified  demand, we could use this sketch and a ruler to find the solution.

^Ø   That is, we could assume an incremental cost rate (λ) and find the power outputs of each of the three units for this value of incremental cost. the three units for this value of incremental cost.

^Ø   Of course, our first estimate will be incorrect.

^Ø   If we have assumed the value of incremental cost such that the total power output is too low, we must increase the 3. value and try another solution.

^Ø   With two solutions, we can extrapolate (or interpolate) the two solutions to get closer to the desired value of total received power.

^Ø   By keeping track of the total demand versus the incremental cost, we can rapidly find the desired operating point.

^Ø   If we wished, we could manufacture a whole series of tables that would show the total power supplied for different incremental cost levels and combinations of units.

^Ø   That is, we will now establish a set of logical rules that would enable us to accomplish the same objective as we have just done with ruler and graph paper.

^Ø   The actual details of how the power output is established as a function of the incremental cost rate are of very little importance.

^Ø   We could, for example, store tables of data within the computer and interpolate between the stored power points to find exact power output for a specified value of incremental cost rate.

^Ø   Another approach would be to develop an analytical function for the power output as a function of the incremental cost rate, store this function (or its coefficients) in the computer, and use this to establish the output of each of the individual units.

^Ø   This procedure is an iterative type of computation, and we must establish stopping rules.

^Ø   Two general forms of stopping rules seem appropriate for this application.

^Ø   The lambda- iteration procedure converges very rapidly for this particular type of optimization problem.

^Ø   The actual computational procedure is slightly more complex than that indicated ,since it is necessary to observe the operating limits on each of the units during the course of the computation.

^Ø   The well-known Newton-Raphson method may be used to project the incremental cost value to drive the error between the computed and desired generation to zero.