Tutorial problems and worked out examples - Principles of Compiler Design

TUTORIAL PROBLEMS AND WORKED OUT EXAMPLES

Problem 1

Table-based LL(1) Predictive Top-Down Parsing

Consider the following CFG G = (N={S, A, B, C, D}, T={a,b,c,d}, P, S) where the set of

productions P is given below: S → A

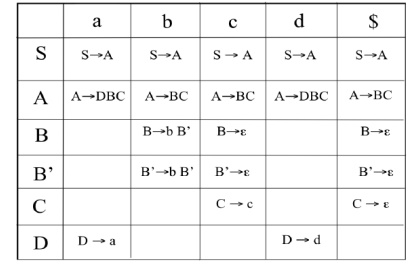
A → BC | DBC

B → Bb | ε

C → c | ε

D → a | d

a) Is this grammar suitable to be parsed using the recursive descendent parsing method? Justify and modify the grammar if needed.

b) Compute the FIRST and FOLLOW set of non-terminal symbols of the grammar resulting from your answer in a)

c) Show the stack contents, the input and the rules used during parsing for the input w = dbb

d) Construct the corresponding parsing table using the predictive parsing LL method.

Answers:

a) No because it is left-recursive. You can expand B using a production with B as the left-most

symbol without consuming any of the input terminal symbols. To eliminate this left recursion we add another non-terminal symbol, B’ and productions as follows:

S → A

A → BC | DBC

B → bB’ | ε

B’ → bB’ | ε

C → c | ε

D → a | d

b) FIRST(S) = { a, b, c, d, ε } FOLLOW(S) = { $ } FIRST(A) = { a, b, c, d, ε } FOLLOW(A) = { $ } FIRST(B) = { b, ε } FOLLOW(B) = { c, $ } FIRST(B’) = { b, ε } FOLLOW(B’) ={ c, $ } FIRST(C) = { c, ε } FOLLOW(C) = { $ }

FIRST(D) = { a, d } FOLLOW(D) = { b, c, $ } Non-terminals A, B, B’, C and S are all nullable.

c) The stack and input are as shown below using the predictive, table-driven parsing algorithm:

d) The parsing table is as shown below:

Problem 2

Perform left recursion and left factoring. S → ( )

S → a

S → ( A ) A → S

A → A , S

Answer

S → ( S’ S → a S’ → ) S’ → A ) A → SA’

A’ → ,SA’ A’ → ε

Problem 3

Eliminate immediate left recursion for the following grammar E->E+T | T, T->T * F | F, F-> (E) | id.

Answer

The rule to eliminate the left recursion is A->Aα|β can be converted as A-> βA’ and A’-> αA’|ε. So, the grammar after eliminating left recursion is

E->TE’; E’->+TE’| ε; T->FT’; T’->*FT’ | ε; F-> (E) | id.

Problem 4

Perform backpatching for the source code:

if a or b then

if c then Answer

x= y+1 After Backpatching:

Translation: 100: if a goto 103

if a go to L1 101: if b goto 103

if b go to L1 102: goto 106

go to L3 103: if c goto 105

L1: if c goto L2 104: goto 106

goto L3 105: x=y+1

L2: x= y+1 106:

L3:

Problem 5

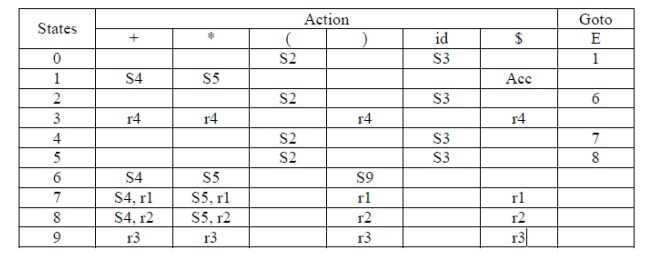
Find the SLR parsing table for the given grammar and parse the sentence (a+b)*c. E->E+E | E*E | (E) | id.

Answer

Given grammar:

1. E->E+E

2. E->E*E

3. E->(E)

4. E->id

Augmented grammar

E’->E

E->E+E

E->E*E

E->(E)

E->id

I0: E’->.E

E->.E+E

E->.E*E

E->.(E)

E->.id

I1: goto(I0, E)

E’->E.

E->E.+E

E->E.*E

I2: goto(I0, ()

E->(.E)

E->.E+E

E->.E*E

E->.(E)

E->.id

I3: goto(I0, id)

E->id.

I4: goto(I1, +)

E->E+.E

E->.E+E

E->.E*E

E->.(E)

E->.id

I5: goto(I1, *)

E->E*.E

E->.E+E

E->.E*E

E->.(E)

E->.id

I6: goto(I2, E)

E->(E.)

E->E.+E

E->E.*E

I7: goto(I4, E)

E->E+E.

E->E.+E

E->E.*E

I8: goto(I5, E)

E->E*E.

E->E.+E

E->E.*E goto(I2, ()=I2 goto(I2, id)=I3