Principal Sources of Optimisation

PRINCIPAL SOURCES OF OPTIMISATION

A transformation of a program is called local if it can be performed by looking only at the statements in a basic block; otherwise, it is called global. Many transformations can be performed at both the local and global levels. Local transformations are usually performed first.

Function-Preserving Transformations

There are a number of ways in which a compiler can improve a program without changing the function it computes.

Function preserving transformations examples:

Common sub expression elimination

Copy propagation,

Dead-code elimination

Constant folding

The other transformations come up primarily when global optimizations are performed.

Frequently, a program will include several calculations of the offset in an array. Some of the duplicate calculations cannot be avoided by the programmer because they lie below the level of detail accessible within the source language.

***

Common Sub expressions elimination:

•      An occurrence of an expression E is called a common sub-expression if E was previously computed, and the values of variables in E have not changed since the previous computation. We can avoid recomputing the expression if we can use the previously computed value.

•   For example

t1: = 4*i

t2: = a [t1]

t3: = 4*j

t4: = 4*i

t5: = n

t6: = b [t4] +t5

The above code can be optimized using the common sub-expression elimination as

t1: = 4*i

 t2: = a [t1]

t3: = 4*j

t5: = n

t6: = b [t1] +t5

The common sub expression t4: =4*i is eliminated as its computation is already in t1 and the value of i is not been changed from definition to use.

Copy Propagation:

Assignments of the form f : = g called copy statements, or copies for short. The idea behind the copy-propagation transformation is to use g for f, whenever possible after the copy statement f: = g. Copy propagation means use of one variable instead of another. This may not appear to be an improvement, but as we shall see it gives us an opportunity to eliminate x.

• For example:

x=Pi;

A=x*r*r;

The optimization using copy propagation can be done as follows: A=Pi*r*r;

Here the variable x is eliminated

Dead-Code Eliminations:

A variable is live at a point in a program if its value can be used subsequently; otherwise, it is dead at that point. A related idea is dead or useless code, statements that compute values that never get used. While the programmer is unlikely to introduce any dead code intentionally, it may appear as the result of previous transformations.

Example:

i=0;

if(i=1)

{

a=b+5;

}

Here, ‘if’ statement is dead code because this condition will never get satisfied.

Constant folding:

Deducing at compile time that the value of an expression is a constant and using the constant instead is known as constant folding. One advantage of copy propagation is that it often turns the copy statement into dead code.

For example,

a=3.14157/2 can be replaced by

a=1.570 there by eliminating a division operation.

Loop Optimizations:

In loops, especially in the inner loops, programs tend to spend the bulk of their time. The running time of a program may be improved if the number of instructions in an inner loop is decreased, even if we increase the amount of code outside that loop.

Three techniques are important for loop optimization:

Ø     Code motion, which moves code outside a loop;

Ø     Induction-variable elimination, which we apply to replace variables from inner loop.

Ø     Reduction in strength, which replaces and expensive operation by a cheaper one, such as a multiplication by an addition.

Fig. 5.2 Flow graph

Code Motion:

An important modification that decreases the amount of code in a loop is code motion. This transformation takes an expression that yields the same result independent of the number of times a loop is executed (a loop-invariant computation) and places the expression before the loop. Note that the notion “before the loop” assumes the existence of an entry for the loop. For example, evaluation of limit-2 is a loop-invariant computation in the following while-statement:

while (i <= limit-2) /* statement does not change limit*/

Code motion will result in the equivalent of

t= limit-2;

while (i<=t) /* statement does not change limit or t */

Induction Variables :

Loops are usually processed inside out. For example consider the loop around B3. Note that the values of j and t4 remain in lock-step; every time the value of j decreases by 1, that of t4 decreases by 4 because 4*j is assigned to t4. Such identifiers are called induction variables.

When there are two or more induction variables in a loop, it may be possible to get rid of all but one, by the process of induction-variable elimination. For the inner loop around B3 in Fig.5.3 we cannot get rid of either j or t4 completely; t4 is used in B3 and j in B4.

However, we can illustrate reduction in strength and illustrate a part of the process of induction-variable elimination. Eventually j will be eliminated when the outer loop of B2- B5 is considered.

Example:

As the relationship t4:=4*j surely holds after such an assignment to t4 in Fig. and t4 is not changed elsewhere in the inner loop around B3, it follows that just after the statement j:=j-1 the relationship t4:= 4*j-4 must hold. We may therefore replace the assignment t4:= 4*j by t4:= t4-4. The only problem is that t4 does not have a value when we enter block B3 for the first time. Since we must maintain the relationship t4=4*j on entry to the block B3, we place an initializations of t4 at the end of the block where j itself is initialized, shown by the dashed addition to block B1 in Fig.5.3.

The replacement of a multiplication by a subtraction will speed up the object code if multiplication takes more time than addition or subtraction, as is the case on many machines.

Reduction In Strength:

Reduction in strength replaces expensive operations by equivalent cheaper ones on the target machine. Certain machine instructions are considerably cheaper than others and can often be used as special cases of more expensive operators. For example, x² is invariably cheaper to implement as x*x than as a call to an exponentiation routine. Fixed-point multiplication or division by a power of two is cheaper to implement as a shift. Floating-point division by a constant can be implemented as multiplication by a constant, which may be cheaper.

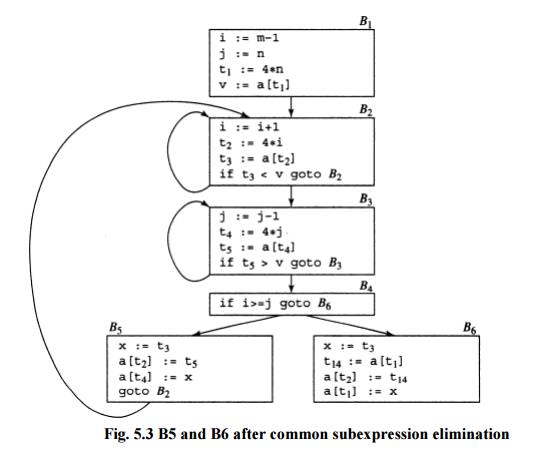
Fig. 5.3 B5 and B6 after common subexpression elimination