Train Resistance Due to Wind

Various forces offer resistance to the movement of a train on the track. These resistances may be a result of the movement of the various parts of the locomotives as well as the friction between them, the irregularities in the track profile, or the atmospheric resistance to a train moving at great speed. The tractive power of a locomotive should be adequate enough to overcome these resistances and haul the train at a specified speed.

Resistance Due to Wind

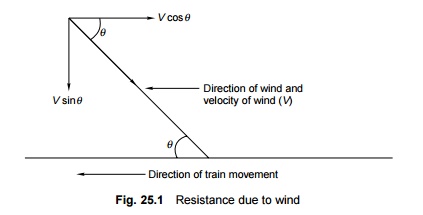
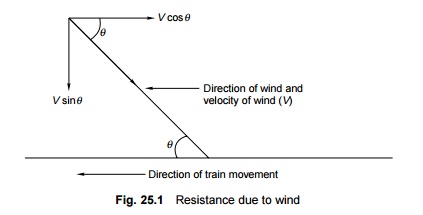
When a vehicle moves with speed, a certain resistance develops, as the vehicle has to move forward against the wind. Wind resistance consists of side resistance, head resistance, and tail resistance, but its exact magnitude depends upon the size and shape of the vehicle, its speed, and wind direction as well as velocity. Wind resistance depends upon the exposed area of the vehicle and the velocity and direction of the wind. In Fig. 25.1, V is the velocity of wind at an angle q . The horizontal component of wind, V cosq , opposes the movement of the train. Wind normally exerts maximum pressure when it acts at an angle of 60 o to the direction of the movement of the train.

Wind resistance can be obtained by the following formula:        

R₃ = 0.000017AV²  (25.3)

where A is the exposed area of vehicle (m²) and V is the velocity of wind (km/h).

Studies also support the fact that the important factors that affect wind resistance are the exposed area of the vehicle and the relative velocity of the wind vis-à-vis that of the vehicle. In fact, wind resistance depends upon the square root of the velocity of the wind. The following formula has been empirically established on the basis of studies.

where R₃ is the wind resistance in tonnes, V is the velocity of the train in km/h, and W is the weight of the train in tonnes.