Hauling Power of a Locomotive

Hauling Power of a Locomotive

The hauling power of a locomotive depends upon the weight exerted on the driving wheels and the friction between the driving wheel and the rail. The coefficient of friction depends upon the speed of the locomotive and the condition of the rail surface. The higher the speed of the locomotive, the lower the coefficient of friction, which is about 0.1 for high speeds and 0.2 for low speeds. The condition of the rail surface, whether wet or dry, smooth or rough, etc., also plays an important role in deciding the value of the coefficient of function. If the surface is very smooth, the coefficient of friction will be very low.

Hauling power = number of pairs of driving wheels × weight exerted on the driving wheels × coefficient of friction

Thus, for a locomotive with three pairs of driving wheels, an axle load of 20 t, and a coefficient of friction equal to 0.2, the hauling power will be equal to 3 × 20 × 0.2 t, i.e., 12 t.

Example 25.2 Calculate the maximum permissible load that a BG locomotive with three pairs of driving wheels bearing an axle load of 22 t each can pull on a straight level track at a speed of 80 km/h. Also calculate the reduction in speed if the train has to run on a rising gradient of 1 in 200. What would be the further reduction in speed if the train has to negotiate a 4 o curve on the rising gradient? Assume the coefficient of friction to be 0.2.

Solution

(a)  Hauling power of the locomotive = number of pairs of driving wheels × wt exerted on each pair × coefficient of friction = 3 × 22 × 0.2 = 13.2 t

(b) The total resistance negotiated by the train on a straight level track at a speed of 80 km/h:

R = Resistance due to friction + resistance due to wave action and track irregularities + resistance due to wind

= 0.0016W + 0.00008WV + 0.0000006WV² Substituting the value of V = 80 km/h

R = 0.01184W

Assuming total resistance = hauling power, W × 0.01184 = 13.2 t

or

W =  13.2   / 0.01184 = 1114.86 t  Approx. 1115 t

On a gradient of 1 in 200, there will be an additional resistance due to gradient equal to W × % of slope. Since hauling power = total resistance,

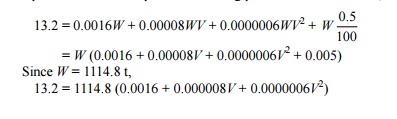
On solving the equation further,

V = 48.13 km/h

Reduction in speed = 80 - 48.13 = 31.87 km/h = 32 km/h

(d) On a curve of 4 o on a rising gradient of 1 in 200, curve resistance will be equal to

R = 0.0004 × degree of curve × wt

= 0.0004 × 4 ×   W = 0.0016W

Hauling power of locomotive = total resistance. Therefore,

13.2 = 0.0016W + 0.00008WV + 0.0000006WV² + 0.005W + 0.0016W By substituting the value of W = 1114.8 t in the equation and solving further,

V = 43.68 km/h

Further reduction in speed = 48.13 - 43.68 = 4.45 km/h. Therefore, Maximum permissible train load = 1115 t

Reduction in speed due to rising gradient = 31.87 t Further reduction in speed due to curvature = 4.45 km/h

Example 25.3 Compute the steepest gradient that a train of 20 wagons and a locomotive can negotiate given the following data: weight of each wagon = 20 t, weight of locomotive = 150 t, tractive effort of locomotive = 15 t, rolling resistance of locomotive = 3 kg/t, rolling resistance of wagon = 2.5 kg/t, speed of the train = 60 km/h.

Solution

(a)  Rolling resistance due to wagons = rolling resistance of wagon × weight of wagon × number of wagons

= 2.5 × 20 × 20 = 1000 kg = 1 t

(b) Rolling resistance due to locomotive

= rolling resistance of locomotive × wt of locomotive

= 3 × 150 = 450 kg = 0.45 t

(c)  Total rolling resistance = rolling resistance due to wagons + rolling resistance due to locomotive = 1.00 + 0.45 t = 1.45 t

(d) Total weight of train = weight of all wagons + wt of locomotive

= 20 × 20 + 150 = 550 t

(e)  Total train resistance = rolling resistance + resistance dependent on speed + resistance due to wind + resistance due to gradient

= 1.45 + 0.00008WV + 0.0000006WV² + W/g

= 1.45 + 0.00008 × 550 × 60 + 0.0000006 × 550 × 60 ² + (550/g) = 1.45 + 2.64 + 1.19 + (550/g) = 5.28 + (550/g)

where g is the gradient.

(f) Tractive effort of locomotive = Total train resistance 15 = 5.28 + (550/g)

or

g = 56.5

= 1/56 = 1 in 56

Therefore, the steepest gradient that the train will be able to negotiate is 1 in 56.

Example 25.4 Calculate the maximum permissible train load that can be pulled by a locomotive with four pairs of driving wheels with an axle load of 28.42 t each on a BG track with a ruling gradient of 1 in 200 and a maximum curvature of 3 o , travelling at a speed of 48.3 km/h. Take the coefficient of friction to be 0.2.

Solution

(a)  Hauling capacity of locomotive

= no. of pairs of driving wheels × axle load × coefficient of friction

= 4 × 28.42 × 0.2 = 22.736 t

(b) Total resistance of train = resistance due to friction + resistance due to speed

+ resistance due to wind + resistance due to gradient + resistance due to curve

= 0.0016W + 0.00008WV + 0.0000006WV² + W(1/g) + 0.0004WD

=0.0016W + 0.00008W × 48.3 + 0.0000006 W × (48.3) ² + W ×

(1/200) × 0.0004 ×  W × 3

(c) Hauling capacity = total resistance 22.73 = 0.01306W

or

W = 1740 t

Therefore, the maximum weight of the train is 1740 t.