Train Resistance Due to Gradient

Various forces offer resistance to the movement of a train on the track. These resistances may be a result of the movement of the various parts of the locomotives as well as the friction between them, the irregularities in the track profile, or the atmospheric resistance to a train moving at great speed. The tractive power of a locomotive should be adequate enough to overcome these resistances and haul the train at a specified speed.

Resistance Due to Gradient

When a train moves on a rising gradient, it requires extra effort in order to move against gravity as shown in Fig. 25.2.

Assuming that a wheel of weight W is moving on a rising gradient OA, the following forces act on the wheel.

(a)  Weight of the wheel (W), which acts downward

(b) Normal pressure N on the rail, which acts perpendicular to OA

(c)  Resistance due to rising gradient (R₄), which acts parallel to OA

These three forces meet at a common point Q and the triangle QCD can be taken as a triangle of forces. It can also be geometrically proved that the two triangles QCD and AOB are similar. From D QCD,

R = W sin q

From D OAB,

R = W ´ AB / OA

In actual practice, the gradients are very small and, therefore, OA is approximately equal to OB. Therefore,

This means that if the weight of the train is 50 t and the slope is 1 in 50 (2%), the resistance due to gradient is

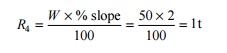
It may be noted here that when a train ascends a slope, extra effort is required to overcome the resistance offered by the gradient. The position is, however, reversed when the train descends a slope and the resistance offered by the gradient helps in the movement of the train.