Chapter: High Voltage Engineering : Electrical breakdown is gases, solids& Liquids
TownsendŌĆÖs Criterion
TOWNSENDŌĆÖS CRITERION
1. Townsend first ionization coefficient
In the absence of electric field the rate of electron and positive ion generation in an ordinary gas is counterbalanced by decay processes and a state of equilibrium exists. This state of equilibrium will be upset upon the application of a sufficiently high field. The variation of the gas current measured between two parallel plate electrodes was first studied as a function of the applied voltage by Townsend.
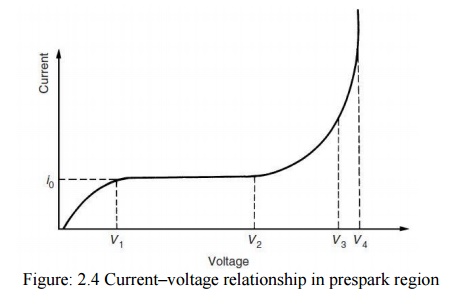
Townsend found that the current at first increased proportionately with the applied voltage and then remained nearly constant at a value i0 which corresponded to the background current (saturation current), or if the cathode was irradiated with a u.v. light, i0 gave the emitted photocurrent. At still higher voltage the current increased above the value i0 at an exponential rate. The general pattern of the currentŌĆōvoltage relationship is shown schematically in Fig. 2.4.
The increase in current beyond V2 Townsend ascribed to ionization of the gas by electron collision. As the field increases, electrons leaving the cathode are accelerated more and more between collisions until they gain enough energy to cause ionization on collision with gas molecules or atoms.

To explain this current increase Townsend introduced a quantity ╬▒, known as TownsendŌĆÖs first ionization coefficient, defined as the number of electrons produced by an electron per unit length of path in the direction of the field. Thus if we assume that n is the number of electrons at a distance x from the cathode in field direction (Fig. 2.5) the increase in electrons dn in additional distance dx is given by

where n0 is the number of primary electrons generated at the cathode. In terms of current, with I0 the current leaving the cathode, eqn (2.10) becomes

The term e╬▒d is called the electron avalanche and it represents the number of electrons produced by one electron in travelling from cathode to anode. The electron multiplication within the avalanche is shown diagrammatically in Fig. 2.3.
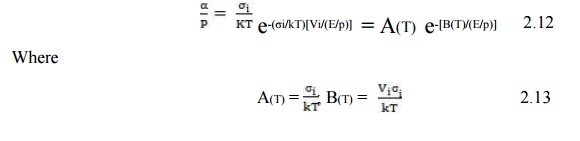
Where A & B are the Ionization Constants.
It cannot be expected that the real dependence of ╬▒/p upon E/p agrees with measured values within the whole range of E/p, because phenomena which have not been taken into account are influencing the ionization rate. However, even with constant values of A and B, eqn (5.47) determines the ionization process within certain ranges of E/p. Therefore, for various gases the ŌĆśconstantsŌĆÖ A and B have been determined experimentally and can be found in the literature.
The constants A and B in eqn (2.13), as derived from kinetic theory, rarely agree with the experimentally determined values. The reasons for this disagreement lies in the assumptions made in our derivations. We assumed that every electron whose energy exceeds eVi will automatically lead to ionization. In reality the probability of ionization for electrons with energy just above the ionization threshold is small and it rises slowly to a maximum value of about 0.5 at 4 to 6 times the ionization energy. Beyond that it decreases. We have also assumed that the mean free path is independent of electron energy which is not necessarily true. A rigorous treatment would require taking account of the dependence of the ionization cross-section upon the electron energy.
2. Townsend Second Ionisation Coefficient
From the equation
I = I0
e╬▒x We have, taking log on both the sides.
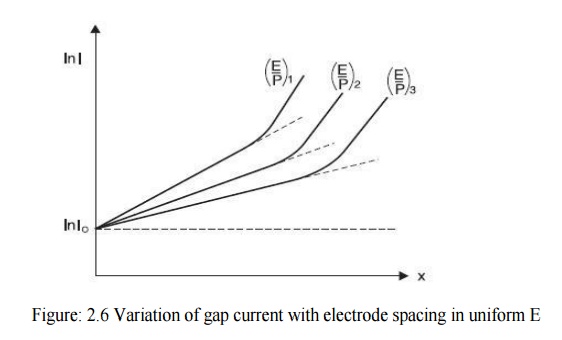
ln I = ln I0 + ╬▒x 2.14
This is a straight line equation with slope ╬▒ and intercept ln I0 as shown in Fig. 2.5 if for a given pressure p, E is kept constant.
Townsend in his earlier investigations had observed that the current in parallel plate gap increased more rapidly with increase in voltage as compared to the one given by the above equation. To explain this departure from linearity, Townsend suggested that a second mechanism must be affecting the current. He postulated that the additional current must be due to the presence of positive ions and the photons. The positive ions will liberate electrons by collision with gas molecules and by bombardment against the cathode. Similarly, the photons will also release electrons after collision with gas molecules and from the cathode after photon impact.
Let us consider the phenomenon of self-sustained discharge where the electrons are released from the cathode by positive ion bombardment. Let n0 be the number of electrons released from the cathode by ultraviolet radiation, n+ the number of electrons released from the cathode due to positive ion bombardment and n the number of electrons reaching the anode. Let ╬Į, known as Townsend second ionization co-efficient be defined as the number of electrons released from cathode per incident positive ion, Then
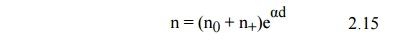
Now total number of electrons released from the cathode is (n0 + n+) and those reaching the anode are n, therefore, the number of electrons released from the gas = n ŌĆō (n0 + n+), and corresponding to each electron released from the gas there will be one positive ion and assuming each positive ion releases ╬Į effective electrons from the cathode then
n+ = vn ŌĆō vn0 ŌĆō vn+
Substituting n+ for n, we have
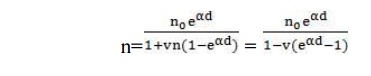
In practice positive ions, photons and metastable, all the three may participate in the process of ionization. It depends upon the experimental conditions. There may be more than one mechanism producing secondary ionization in the discharge gap and, therefore, it is customary to express the net secondary ionization effect by a single coefficient v and represent the current by the above equation keeping in mind that ╬Į may represent one or more of the several possible mechanism.
╬Į = ╬Į1 + ╬Į2 + ╬Į3 +.....
It is to be noted that the value of ╬Į depends upon the work function of the material. If the work function of the cathode surface is low, under the same experimental conditions will produce more emission. Also, the value of ╬Į is relatively small at low value of E/p and will increase with increase in E/p.
This is because at higher values of E/p, there will be more number of positive ions and photons of sufficiently large energy to cause ionization upon impact on the cathode surface. It is to be noted that the influence of ╬Į on breakdown mechanism is restricted to Townsend breakdown mechanism i.e., to low-pressure breakdown only.
3. Townsend Breakdown Mechanism
When voltage between the anode and cathode is increased, the current at the anode is given by

The current in the anode equals the current in the external cirrcuit. Theoretically the current becomes infinitely large under the above mentioned condition but practically it is limited by the resistance of the external circuit and partially by the voltage drop in the arc.
The condition ╬Įe╬▒d = 1 defines the condition for beginning of spark and is known as the Townsend criterion for spark formation or Townsend breakdown criterion. Using the above equations, the following three conditions are possible.

The number of ion pairs produced in the gap by the passage of arc electron avalanche is sufficiently large and the resulting positive ions on bombarding the cathode are able to relase one secondary electron and so cause a repetition of the avalanche process. The discharge is then said to be self-sustained as the discharge will sustain itself even if the source producing I is removed. Therefore, the condition ╬Įe╬▒d = 1 defines the threshold sparking condition.
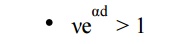
Here ionization produced by successive avalanche is cumulative. The spark discharge grows more rapidly the more ╬Įe╬▒d exceeds unity.
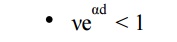
Here the current I is not self-sustained i.e., on removal of the source the current I0 ceases to flow.
Related Topics