Chapter: High Voltage Engineering : Electrical breakdown is gases, solids& Liquids
Thermal Breakdown
THERMAL BREAKDOWN
When an
insulating material is subjected to an electric field, the material gets heated
up due to conduction current and dielectric losses due to polarization. The
conductivity of the material increases with increase in temperature and a
condition of instability is reached when the heat generated exceeds the heat
dissipated by the material and the material breaks down.
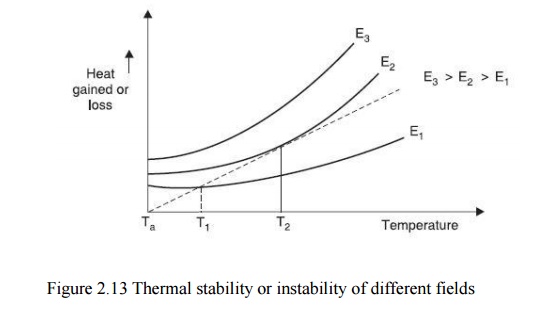
Fig. 2.13
shows various heating curves corresponding to different electric stresses as a
function of specimen temperature. Assuming that the temperature difference
between the ambient and the specimen temperature is small, NewtonŌĆÖs law of
cooling is represented by a straight line.
The test
specimen is at thermal equilibrium corresponding to field E1 at temperature
T1 as beyond that heat generated is less than heat lost. Unstable
equilibrium exists for field E2 at T2,
and for
field E3 the state of equilibrium is never reached and hence the
specimen breaks down thermally.
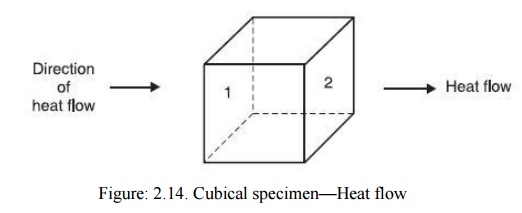
In order
to obtain basic equation for studying thermal breakdown, let us consider a
small cube (Fig. 2.14) within the dielectric specimen with side Δx and
temperature difference across its faces in the direction of heat flow (assume
here flow is along x-direction) is ΔT. Therefore, the temperature gradient is

Here the
second term indicates the heat input to the differential specimen. Therefore,
the heat absorbed by the differential cube volume
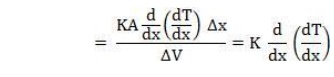
The heat
input to the block will be partly dissipated into the surrounding and partly it
will raise the temperature of the block. Let CV be the thermal
capacity of the dielectric, Žā the electrical conductivity, E the electric field
intensity. The heat generated by the electric field = ŽāE2 watts, and
suppose the rise in temperature of the block is ΔT, in time dt, the power
required to raise the temperature of the block by ΔT is
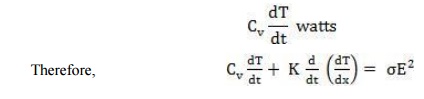
The
solution of the above equation will give us the time required to reach the
critical
temperature
Tc for which thermal instability will reach and the dielectric will
lose its insulating properties.
However,
unfortunately the equation can be solved in its present from CV, K
and Žā is all functions of temperature and in fact Žā may also depend on the
intensity of electrical field.
Therefore,
to obtain solution of the equation, we make certain practical assumptions and
we consider two extreme situations for its solution
Table:
2.3 Thermal breakdown voltage

Table 2.3
gives for thick specimen, thermal breakdown values for some dielectric under
a.c. and d.c. voltages at 20┬░C.
Related Topics