Torsion: Membrane Analogy

Membrane Analogy

The crucial step in the stress-function approach, finding ϕ, is not much easier than finding a warping function w. Its advantage comes from the simple

boundary condition and, more importantly, the aid it gives in visualizing the stress-function hill by analogy. In his presentation in 1903, Prandtl* observed that the stress-function equation Ɐ²ϕ= -2Gθ is the same Poisson type as that giving the elevation of an elastic membrane loaded by pressure on one side. While the computer with canned finite-difference or finite element solutions to Poisson’s equation have replaced actual laboratory experiments with soap films, the membrane analogy is an extremely useful heuristic device to visualize the ϕ surface and hence the stiffness of and the shear stresses on a cross-section under torque. In most cases, in fact, approximate calculations based on the membrane analogy are more than adequate for rough analysis and design.

As shown in Figure 9.8, imagine a flexible membrane stretched flat over a hole in a flat plate of the irregular shape of the cross-section to be analyzed. Air pressure is applied and the membrane is stretched a distance z(x,y) above the plate. Summing forces in the z direction:

gives the resultant shearing stress at any point.

Thus the tangent to any membrane contour gives the direction of the result-ant shear with a magnitude equal to the slope perpendicular to the contour line at that point. The twisting movement

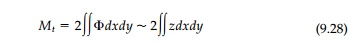
is twice the volume under the membrane. Finally, if we consider vertical equilibrium along a contour s,

When there is a hole in the cross-section, the shear stress must be zero and the membrane must be flat, corresponding to a weightless plate “floating” on

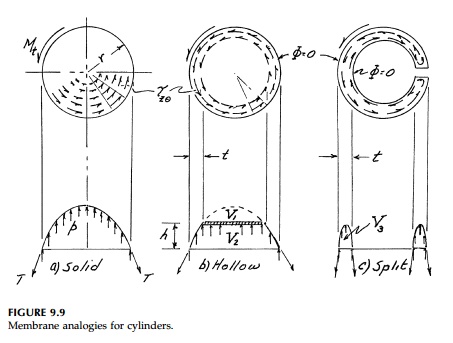
the surface. For example a solid cylinder is compared to hollow and split cyl-inders in Figure 9.9. Clearly, considering the weight reduction, removing the core of a solid cylinder is a good design choice since the reduction in torsional stiffness and moment capacity V₁ compared to V₂ (that remaining) is small.* For the split ring in Figure 9.9 with a moment capacity proportional to the volume of the small torus V₃ , the reduction is dramatic. If the wall thickness is small, a cut reduces the capacity to where it is essentially that of a thin plate of thickness t and length equal to the perimeter 2πr. In fact it is nearly correct for any thin-walled, open cross-section to calculate its moment capacity and stiffness as the sum of its elements considered as flat plates.

It is easy to solve for a flat plate under torsion from the membrane analog. If b > t then, except near the ends, the shape of a nearly “flat” membrane under uniform vertical load on the horizontal projection is parabolic** as shown in Figure 9.10. Thus

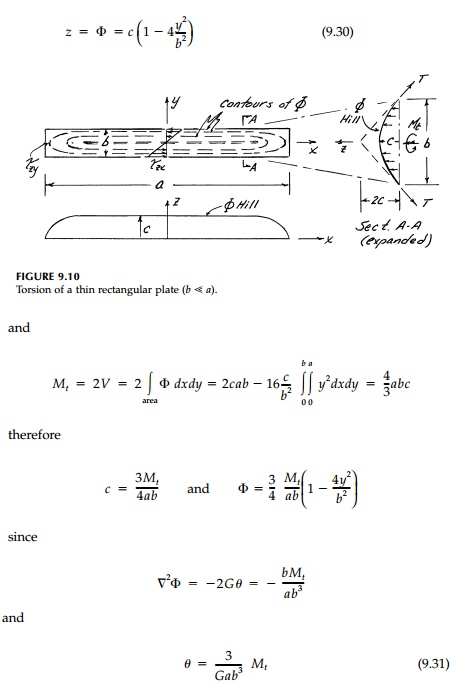
evidently the “torsional constant” (i.e., the shape contribution to the torsional stiffness GJ) is

This result can be generalized to any thin-walled, open section such as shown in Figure 9.11. It is approximately correct to say that the inflated mem-brane shape is parabolic throughout except near the ends and at any corner. Since θ must be the same for each part then:

and the maximum stress will occur where the thickness is a minimum in Equation (9.35).

Corrections for the end and corner effects are possible using, for example, Fourier series or experimental results. Today, however, numerical solutions to Poisson’s equation on the computer will generate results to any degree of precision. Such results are shown in Table 9.1. It is interesting that computing power and more exact solutions, if anything, only increase the necessity for the designer to understand the membrane analogy in order to visualize the results and then shape