Thin Walled Tubes of Arbitrary Shape

Thin Walled Tubes of Arbitrary Shape

The membrane analogy is also very useful in analyzing torsion of thin tubes of arbitrary shape with variable thickness that is “small” in comparison to the overall dimensions. Because t is small, the curvature of the membrane

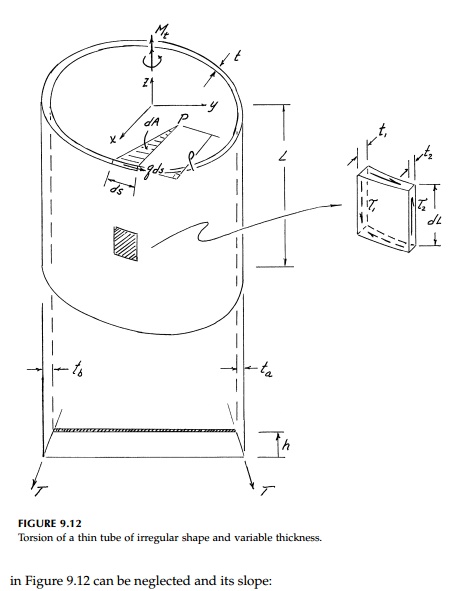
where A is the area enclosed by the average perimeter. Therefore, the shear stress

and therefore, from a design standpoint, a circular tube of constant thickness is optimum since it has the maximum area for a given weight of material to sustain the constant shear stress.* To determine the angle of twist we can apply, Equation (9.29)

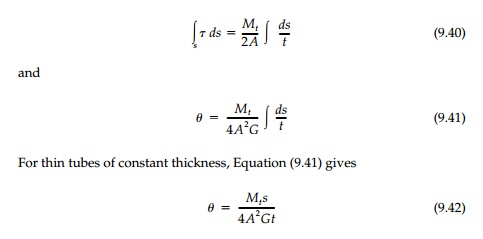
It is important to note that this analysis, in which we have used the mem-brane analogy can, just as well, be derived from statics alone. As shown in Figure 9.12, longitudinal equilibrium of a slice in the z direction requires that

Now taking moments about any arbitrary point P in the plane of the cross-section:

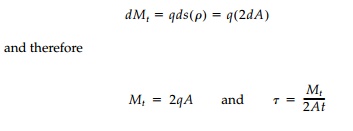
where A is the total area enclosed by the cross-section (as in the membrane analogy) and not the cross-sectional area of the wall of the tube.

Thus the special case of torsion of a thin tube is statically determinate. As we will see later, this allows us to use this solution as a building block to generate lower-bound estimates of the plastic behavior of all sorts of cross-sections in torsion.

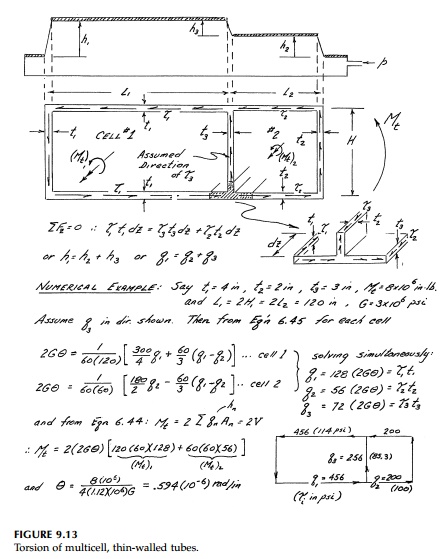
Multicell thin tubes, which occur in box bridges, aircraft, cars, ships, and skyscrapers can be analyzed with a simple extension of the single-cell approach and the shear flow concept. An example with small wall thick-nesses is shown in Figure 9.13. From the membrane analogy

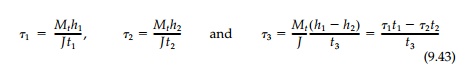
and the twisting moment equals twice the volume under the membrane or

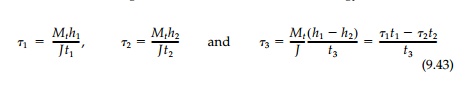
From Equation (9.40) assuming t₁, t₂, and t₃ are constant

Again it should be noted that Equation (9.43) can, as shown in Figure 9.13, be thought of as the equilibrium condition at a junction in the longitudinal direction where:

and q = τt is a constant in any branch. This is also the continuity equation for fluid flow in a channel or pipe network stating that the amount of liquid com-ing into a junction must equal that flowing out. Hence the hydrodynamic analogy and the term “shear flow” for q.