Thin Cylinders, Spheres and Thick Cylinders

THIN CYLINDERS, SPHERES AND THICK CYLINDERS

Triaxial Stress, Biaxial Stress, and Uniaxial Stress

Triaxial stress refers to a condition where only normal stresses act on an element and all shear stresses (t_xy, t_xz, and t_yz) are zero. An example of a triaxial stress state is hydrostatic pressure acting on a small element submerged in a liquid.

A two-dimensional state of stress in which only two normal stresses are present is called biaxial stress. Likewise, a one-dimensional state of stress in which normal stresses act along one direction only is called a uniaxial stress state.

Pure Shear

Pure shear refers to a stress state in which an element is subjected to plane shearing stresses only, as shown in Figure 3. Pure shear occurs in elements of a circular shaft under a torsion load.

Figure 3. Element in pure shear

Thin cylindrical and spherical shells

Thin-walled assumption

For the thin-walled assumption to be valid the vessel must have a wall thickness of no more than about one-tenth (often cited as one twentieth) of its radius. This allows for treating the wall as a surface, and subsequently using the  Young–Laplace equation for estimating the hoop stress created by an internal pressure on a thin wall cylindrical pressure vessel:

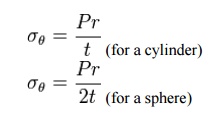
where

·        P is the internal pressure

·        t is the wall thickness

·        r is the inside radius of the cylinder.

·          Ro Deta is the hoop stress.

The hoop stress equation for thin shells is also approximately valid for spherical vessels, including plant cells and bacteria in which the internal turgor pressure may reach several atmospheres.

Inch-pound-second system (IPS) units for P are  pounds-force per square inch (psi). Units for t, and d are inches (in). SI units for P are  pascals (Pa), while t and d=2r are in meters (m).

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

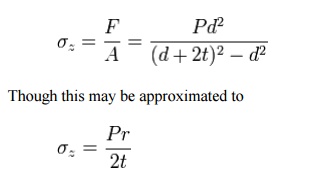
Also in this situation a radial stress  is developed and may be estimated in thin walled cylinders as:

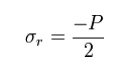
Deformation in thin cylindrical and spherical shells

Thick cylinders and shells

Thick Walled Cylinders

Under the action of radial Pressures at the surfaces, the three Principal Stresses will be . These Stresses may be expected to vary over any cross-section and equations will be found which give their variation with the radius r.

It is assumed that the longitudinal Strain e is constant. This implies that the cross-section remains plain after straining and that this will be true for sections remote from any end fixing.

Let u be the radial shift at a radius r. i.e. After Straining the radius r becomes (r + u). and it should be noted that u is small compared to r.

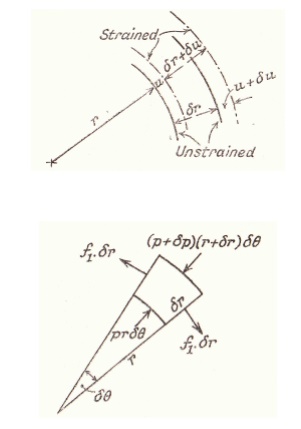
Internal Pressure Only

Pressure Vessels are found in all sorts of engineering applications. If it assumed that the Internal and Pressure is at a diameter of that the external pressure is zero ( Atmospheric) at a diameter then using equation (22)

The Error In The "thin Cylinder" Formula

If the thickness of the cylinder walls is t then and this can be substituted into equation

Which is 11% higher than the mean value given by And if the ratio is 20 then which is 5% higher than

It can be seen that if the mean diameter is used in the thin cylinder formula, then the error is minimal.

Example 1

The cylinder of a Hydraulic Ram has a 6 in. internal diameter. Find the thickness required to withstand an internal pressure of 4 tons/sq.in. The maximum Tensile Stress is limited to 6 tons/sq.in. and the maximum Shear Stress to 5 tons/sq.in.

If D is the external diameter, then the maximum tensile Stress is the hoop Stress at the inside.

Using equation (43)

Stresses on inclined plane

Stresses on inclined plane

procedure to tackle stresses on inclined planes

STEPS:

In order to do achieve the desired objective we proceed in the following manner

(i)       Label the Block ABCD.

(ii)     Set up axes for the direct stress (as abscissa) and shear stress (as ordinate)

(iii)   Plot the stresses on two adjacent faces e.g. AB and BC, using the following sign convention.

tensile positive; compressive, negative Shear stresses –tending to turn block clockwise, positive

–tending to turn block counter clockwise, negative

[ i.e shearing stresses are +ve when its movement about the centre of the element is clockwise ]

This gives two points on the graph which may than be labeled as   respectively to denote stres these planes.

(iv) Join   AB bar and BC bar.

(v) The point P where this line cuts the s axis is than the centre of Mohr's stress circle and th joining  AB bar and BC bar  is diameter. Therefore the circle can now be drawn.

Now every point on the circle then represents a state of stress on some plane through C.

Principal planes and stresses

Principal stresses and planes

Principal Directions, Principal Stress

x' andy' (x'y') vary smoothly with respect to the rotation accordance with the  coordinate transformation equations. There exist a couple of particular angles wher take on special values.

First, there exists an angle p where the shear stress x'y' becomes zero. That angle is found by setting the above shear transformation equation and solving for (set equal to p). The result is,

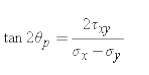
The angle p defines the principal directions where the only stresses are normal stresses. These called principal stresses and are found from the original stresses (expressed in the x,y,z directions) via,

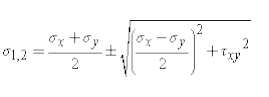
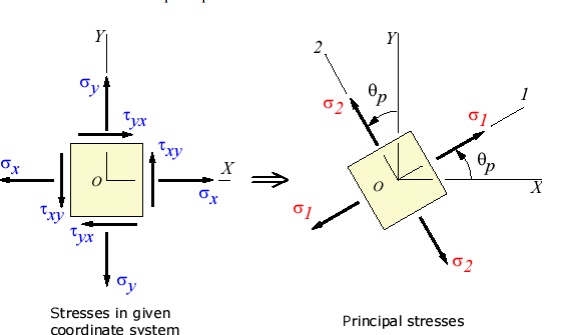
The transformation to the principal directions can be illustrated as:

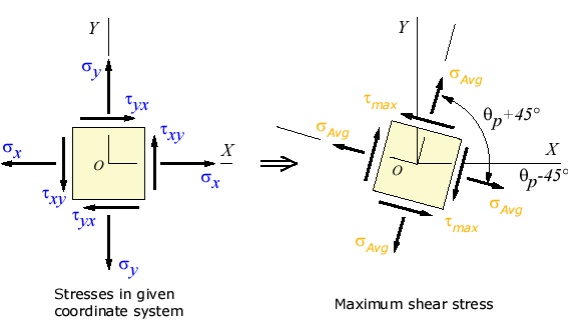
Maximum Shear Stress Direction

s, is where the maximum shear stress occurs. This is found by finding the ma. Another important angle, shear stress transformation equation, and solving for

The maximum shear stress is equal to one-half the difference between the two principal stresses,

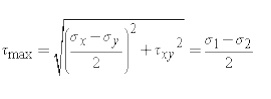
The transformation to the maximum shear stress direction can be illustrated as:

Mohr’s   circle   for   biaxial   stress

To find the maximum and minimum normal stresses throughout the entire range of angles, one can easily take the first derivative of (3) with respect to theta, set it to zero, and solve for the angle. This will give what is called the principal plane on which the principal

stresses act. If this all sounds overly complicated... you're right! Why not just use the tried and true terminology "maximizing and minimizing the function" instead of inventing these two new terms with unrelated and unclear meaning? Well.... that's civil engineers for you.

Where thetap defines the orientation of the principal planes, and its two values, differing by 180o, are called the principal angles.

Now is where we begin to get into the unnecessary jargon. All the excess baggage some engineer created to make it so that utilizing these relationships would not require higher math. This (and many other examples of engineer idioticy) most likely stems from the fact that most engineers slept through their higher level math classes, and suffer from acute mathematical insecurities (and probably rightly so.) It's these abstract constructions which attempt to simplify the work, yet ultimately make it more difficult for those of us more mathematically inclined, that really piss me off. If you represent equation (5) geometrically with a 90o triangle, (left), we can obtain general formulas for the principal stresses. First, we note that the hypotenuse of the triangle is,

R = SQR{ [(Ox - Oy)/2]² + Txy²}     (6)

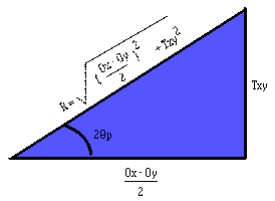
The quantity R is defined as a positive number, and, like the other two sides of the triangle, has the completely meaningless units of "stress". From the triangle we obtain two additional relations:

cos(2theta_p) = (Ox - Oy)/(2R)  sin(2theta_p) = Txy/R      (7, 8)

Which is all very well and good, because it actually leads to the USEFUL equation for the general formula for the principal stresses:

O_1,2 = (Ox + Oy)/2 ⁺/- R        (9)

But such usefulness is short lived as we approach MOHR'S CIRCLE..... Actually, Mohr's circle isn't all that bad in many cases. It supplies its practitioners a clever and easy way to compute otherwise hairy moments of inertia, allows strain analyses to be handled quickly. However, in this case, its application seems to me a bit of a stretch, and what you wind up with is this hopelessly complicated graphical representation that seems so much more difficult than the original equations (3) and (4) that it's hardly worth the effort to learn at all. HOWEVER.... because certain  bastich elements in the civil engineering department here at  the U of A are requiring their students (many of whom, myself included, will NEVER use these relationships again after the class has ended) to use this technique in spite of the fact that we know of a perfectly valid and correct alternative.

The equations of Mohr's circle can be derived from the transformation equations (3) and (4). By simply rearranging the first equation, we find that the two expressions comprise the equation of a circle in parametric form.

Ox₁ - (Ox + Oy)/2 = [(Ox - Oy)/2]cos(2theta) + Txy sin(2theta)  (10)

Tx₁y₁ = - {(Ox - Oy)/2}sin(2theta) + Txy cos(2theta)  (11)

To eliminate the 2theta parameter, we square each relationship and add the two equations together. This ultimately leads to (after simplification),

(Ox₁ - {Ox + Oy}/2)² + Tx₁y₁² = {(Ox - Oy)/2}² + Txy² (12)

However, by resubstitution of equation (6) and by recognizing that the average stress value between the X and Y axis, Oave, is,

Oave = (Ox + Oy)/2

equation (12) can be simplified into the semi friendly equation of a circle in standard algebraic form,

(Ox₁ - Oave)² + Tx₁y₁² = R²       (13)

However, don't let this nice looking equation for a circle fool you. Hidden in this simple equation are some of the most hairy, complicated, and down-right nasty relationships I think I have ever encountered. This makes my studies in the Frobenious theorem for solving differential equations with non-constant singular coefficients seem tame.

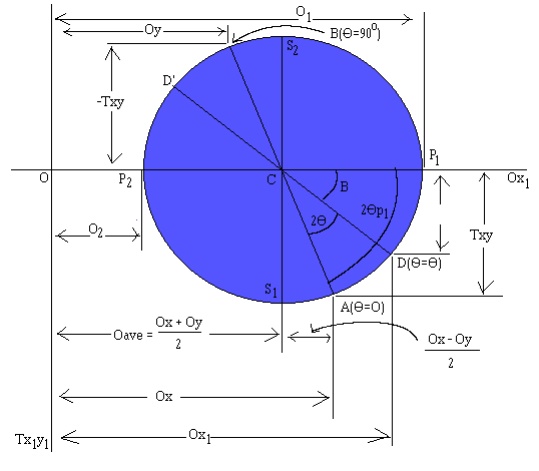
With Ox, Oy, and Txy known, the procedure for constructing Mohr's circle is as follows:

1.     Draw a set of coordinate axis with Ox₁ and Tx₁y₁ (with T positive downwards. From now on, for simplicity, O and T will represent their respective axis.)

2.     The center of the circle, by equation (13) is located at T=0 and O=Oave. Oave is nothing more than (12.a), so the center of the circle is located at:

C = (Ox + Oy)/2

3.     Locate point A, representing the stress conditions on the X face of the normal oriented element (Figure 1, extreme top left, non-rotated section). Plot coordinates O = Ox, T = Txy. Here, it is important to note that at point A, the inclination angle, theta, is zero.

4.     Locate point B, representing the stress conditions on the Y face of the normal oriented element (Figure 1, again, extreme top left, non-rotated section). Again, plot

coordinates O = Oy, T = Txy. Note that this point, B, will be diametrically opposite from point A. Also note, that the angle of inclination at B, theta, will be 90^o, as it could also be achieved on the X face by rotating it by 90^o.

5.     Draw a line from point A to point B through the center C. This line is a diameter of the circle.

6.                       Using point C as the center, draw Mohr's circle through points A and B. The circle will have a radius of R, which is the same R as in equation (6).

Now that you have Mohr's circle drawn, you can use it to analyze the problem. (Remember, that this method is every bit as valid as simply using equations (3) and (4) above, except it requires less mathematical skill, and many more memorized relationships.)

O_1,2, representing the maximum and minimum normal stresses and their respective angles away from point A (where theta = 0^o) can be found by simply looking at the O values when T = 0. In the drawing above, O₁ represents the maximum, and O₂ the minimum.

Furthermore, T_max/min, representing the maximum and minimum shear stresses and their respected angles can be found by locating the T values when O = Oave. At this point, T is

simply equal to the radius, R, or equation (6).

In addition to these helpful points, all other possible points for the shear and normal stresses can be found on this circle. In order to find another value of Ox, Oy for a given rotation, one must simply start at the A and B points (A representing the Ox value and B, the Oy value), and rotate in a positive theta direction (by the orientation shown above, this is in a counterclockwise direction, in keeping with the right hand rule) for 2theta (from equations

(3) and (4) above). The resulting points, D and D', will yield the Ox, Txy, and Oy, Txy (respectively) for that rotation.

As I have likely mentioned before (likely because, I can't really recall) to me this seems all very abstract and difficult to use. However, the aforementioned bastiches will be requiring this on my upcoming test, so I felt a need to more fully understand it. Granted, I still don't understand it as fully as I would hope, but it ought to be enough to get me through this one, insignificant little test.

P.S.: I apologize for my editorializing and opinionated presentation of this topic. I rarely do this when I analyze problems I don't understand (even when I do not like the method, such as the  Lewis Dot structure). This time, however, I have some very strong feelings about my predicament. Also, in all fairness, if you were given the problem where O1 = O2 and Tmax = 0, i.e. the Mohr's circle was simply a little dot with R = 0, using the Mohr's circle method would arrive you at any and all answers much quicker than using equations (3) and (4). However, I don't think this extreme simplification of one special case warrants the abstraction being a required bit of knowledge for civil engineers.