Deformation in thin cylindrical and spherical shells

Deformation in thin cylindrical and spherical shells

Thick cylinders and shells

Thick Walled Cylinders

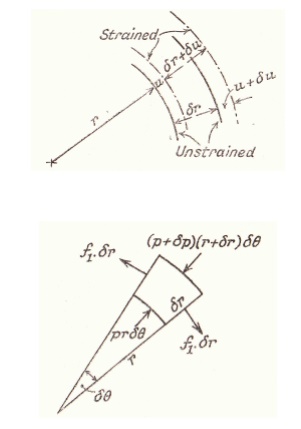
Under the action of radial Pressures at the surfaces, the three Principal Stresses will be . These Stresses may be expected to vary over any cross-section and equations will be found which give their variation with the radius r.

It is assumed that the longitudinal Strain e is constant. This implies that the cross-section remains plain after straining and that this will be true for sections remote from any end fixing.

Let u be the radial shift at a radius r. i.e. After Straining the radius r becomes (r + u). and it should be noted that u is small compared to r.

Internal Pressure Only

Pressure Vessels are found in all sorts of engineering applications. If it assumed that the Internal and Pressure is at a diameter of that the external pressure is zero ( Atmospheric) at a diameter then using equation (22)

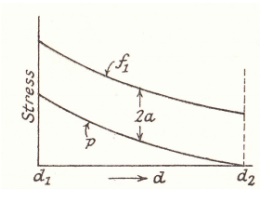
The Error In The "thin Cylinder" Formula

If the thickness of the cylinder walls is t then and this can be substituted into equation

Which is 11% higher than the mean value given by And if the ratio is 20 then which is 5% higher than

It can be seen that if the mean diameter is used in the thin cylinder formula, then the error is minimal.

Example 1

The cylinder of a Hydraulic Ram has a 6 in. internal diameter. Find the thickness required to withstand an internal pressure of 4 tons/sq.in. The maximum Tensile Stress is limited to 6 tons/sq.in. and the maximum Shear Stress to 5 tons/sq.in.

If D is the external diameter, then the maximum tensile Stress is the hoop Stress at the inside.

Using equation (43)