Chapter: Mechanical : Strength of Materials : Thin Cylinders, Spheres and Thick Cylinders
Important Answers: Thin Cylinders, Spheres and Thick Cylinders
THIN CYLINDERS, SPHERES AND THICK
CYLINDERS
1.
List out the modes of failure in thin cylindrical shell due to an internal
pressure.
i)Circumferential or hoop stress and
ii)Longitudinal
stress
2. What do you mean by principal plane?
The
planes which have no shear stress are known as principal planes.
3. What are assumptions involved in the
analysis of thin cylindrical shells?
The material of the cylinder is homogeneous, isotr
i)The hoop stress distribution in thin cylinder is uniform over the cross
section from inner to outer
surface since the thickness of the cylinder is thin
and
ii)Weight
of fluid and material of the cylinder is not taken into account.
4.What are principal planes and
principal stress one end is fixed and other end is free?
Principal stress: The magnitudes of normal stress,
acting on a principal plane are known as principal stresses. The plane which
have no shear stress are known as principal planes.
5. Define Circumferential and Hoop
stress.
A thin cylinder shell is subjected to an internal
pressure, as a result of internal pressure, the cylinder has tendency to split
up into two troughs is called circumferential stress. The same cylinder shell,
subjected to the same internal pressure, the cylinder also has a tendency to
split in to two ieces is known as Hoop stress.
6. What
is the ?use
of Mohr’s
It
is used to find out the normal, tangential, resultant and principal stresses
and their
planes.
7.What are the planes along which the greatest
shear stresses occurs?
Greatest shear stress occurs at the planes which is
inclined at 45Ëšto
its normal.
8.What
is the radius
of Mohr’s ?
Radius of Mohr’s circle is equal to the maximum
shear stress.
9. In case of equal like principal stresses what is
the diameter of the Mohr’s circle?
In case of equal like principal stresses what is the
diameter of the Mohr’s circle is zero.
10. What is mean by position of
principal planes?
The planes on which
shear stress is zero are known as principal planes. The position of principal
planes are obtained by equating the tangential stress to zero.
11. What is solid length?
The
length of a spring under the maximum compression is called its solid length. It
is the product of total number of coils and the diameter of wire.
Ls = nt x d
Where, nt = total number of coils.
12.
Define spring rate (stiffness).
The
spring stiffness or spring constant is defined as the load required per unit
deflection of the spring.
K= W/y Where , W - load
y- Deflection
13. Define pitch.
Pitch of
the spring is defined as the axial distance between the adjacent coils in
uncompressed state. Mathematically
Pitch=free length n-1
14. Define helical
springs.
The
helical springs are made up of a wire coiled in the form of a helix and are
primarily intended for compressive or tensile load.
15. What are the
differences between closed coil & open coil helical springs? Closed coil
spring
The
spring wires are coiled very closely, each turn is nearly at right angles to
the axis of helix . Helix angle is less (70 to 10o)
Open coil spring
The wires
are coiled such that there is a gap between the two consecutive turns. Helix
angle is large (>10o)
16.
Write the assumptions in the theory
of pure torsion.
1. The
material is homogenous and isotropic.
2. The
stresses are within elastic limit
3.
C/S which are plane before applying
twisting moment remain plane even after the application of twisting moment.
4. Radial
lines remain radial even after applying torsional moment.
5. The
twist along the shaft is uniform
17.
Define : Polar Modulus
Polar modulus is
defined as the ratio of polar moment of inertia to extreme radial distance of
the fibre from the centre.
18. Write the equation for the polar
modulus for solid circular section
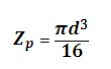
Related Topics