Chapter: Fundamentals of Database Systems : The Relational Data Model and SQL : The Relational Algebra and Relational Calculus
The Tuple Relational Calculus
The Tuple Relational Calculus
In this and the next section, we introduce another formal query language
for the relational model called relational
calculus. This section introduces the language known as tuple relational calculus, and Section
6.7 introduces a variation called domain
relational calculus. In both variations of relational calculus, we write
one declarative expression to
specify a retrieval request; hence, there is no description of how, or in what order, to evaluate a query. A calculus expression specifies
what is to be retrieved rather than how to retrieve it. Therefore, the
relational calculus is considered to be a nonprocedural
language. This differs from relational algebra, where we must write a sequence of operations to specify a
retrieval request in a particular order of applying the operations; thus,
it can be considered as a procedural way of stating a query.
It is possible to nest algebra operations to form a single expression; however,
a certain order among the operations is always explicitly specified in a
relational algebra expression. This order also influences the strategy for
evaluating the query. A calculus expression may be written in different ways,
but the way it is writ-ten has no bearing on how a query should be evaluated.
It has been shown that any retrieval that can be specified in the basic
relational algebra can also be specified in relational calculus, and vice
versa; in other words, the expressive
power of the languages is identical. This led to the definition of
the concept of a relationally complete
language. A relational query language L
is considered relationally complete if
we can express in L
any query that can be expressed in relational calculus. Relational
completeness has become an important basis for comparing the expressive power
of high-level query languages. However, as we saw in Section 6.4, certain
frequently required queries in database applications cannot be expressed in
basic relational algebra or calculus. Most relational query languages are
relationally complete but have more
expressive power than relational algebra or relational calculus because of
additional operations such as aggregate functions, grouping, and ordering. As
we mentioned in the introduction to this chapter, the relational calculus is
important for two reasons. First, it has a firm basis in mathematical logic.
Second, the standard query language (SQL) for RDBMSs has some of its
foundations in the tuple relational calculus.
Our examples refer to the database shown in Figures 3.6 and 3.7. We will
use the same queries that were used in Section 6.5. Sections 6.6.6, 6.6.7, and
6.6.8 discuss dealing with universal quantifiers and safety of expression
issues. (Students inter-ested in a basic introduction to tuple relational
calculus may skip these sections.)
1. Tuple Variables and
Range Relations
The tuple relational calculus is based on specifying a number of tuple variables. Each tuple variable
usually ranges over a particular
database relation, meaning that the variable may take as its value any
individual tuple from that relation. A simple tuple relational calculus query
is of the form:
{t | COND(t)}
where t is a tuple variable
and COND(t) is a conditional (Boolean)
expression involving t that evaluates
to either TRUE or FALSE for different assignments of tuples to the variable t. The result of such a query is the set
of all tuples t that evalu-ate COND(t) to TRUE. These tuples are said to satisfy
COND(t). For example, to find all
employees whose salary is above $50,000, we can write the following tuple
calcu-lus expression:
{t | EMPLOYEE(t) AND t.Salary>50000}
The condition EMPLOYEE(t) specifies that the range
relation of tuple variable t is EMPLOYEE. Each
EMPLOYEE tuple t that satisfies the condition t.Salary>50000
will be retrieved. Notice that t.Salary references attribute Salary of tuple variable t; this notation resembles how attribute
names are qualified with relation names or aliases in SQL, as we saw in Chapter
4. In the notation of Chapter 3, t.Salary is the same as writing t[Salary].
The above query retrieves all attribute values for each selected EMPLOYEE tuple t. To retrieve only some of the attributes—say, the first
and last names—we write
{t.Fname, t.Lname | EMPLOYEE(t) AND t.Salary>50000}
Informally, we need to specify the following information in a tuple
relational calcu-lus expression:
For each tuple variable t, the range relation R of t. This value is specified by a
condition of the form R(t). If we do not specify a range
relation, then the variable t will
range over all possible tuples “in the universe” as it is not restricted to any
one relation.
A condition to select particular
combinations of tuples. As tuple variables range over their respective range
relations, the condition is evaluated for every possible combination of tuples
to identify the selected combinations
for which the condition evaluates to TRUE.
A set of attributes to be
retrieved, the requested attributes.
The values of these attributes are retrieved for each selected combination of
tuples.
Before we discuss the formal syntax of tuple relational calculus,
consider another query.
Query 0. Retrieve the birth date and address of the employee (or employees) whose name is John B. Smith.
Q0: {t.Bdate,
t.Address |
EMPLOYEE(t)
AND t.Fname=‘John’
AND t.Minit=‘B’
AND t.Lname=‘Smith’}
In tuple relational calculus, we first specify the requested attributes t.Bdate and t.Address for each
selected tuple t. Then we specify the
condition for selecting a tuple
following the bar (|)—namely, that t
be a tuple of the EMPLOYEE relation whose Fname, Minit, and Lname attribute values are ‘John’, ‘B’, and ‘Smith’, respectively.
2. Expressions and Formulas
in Tuple Relational Calculus
A general
expression of the tuple relational
calculus is of the form
{t1.Aj, t2.Ak, ..., tn.Am | COND(t1, t2, ..., tn,
tn+1, tn+2, ..., tn+m)}
where t1, t2, ..., tn,
tn+1, ..., tn+m are tuple variables, each Ai is an attribute of the rela-tion on which ti ranges, and COND is a condition or formula.13
of the tuple rela-tional calculus. A formula is made up of predicate calculus atoms, which can be one of the
following:
An atom of the form R(ti), where R is a relation name and ti is a tuple vari-able. This
atom identifies the range of the tuple variable ti as the relation whose name is R. It evaluates to TRUE if ti is a tuple in the relation
R, and evaluates to FALSE otherwise.
An atom of the form ti.A op tj.B, where op is one of the comparison opera-tors in the set {=, <, ≤, >, ≥, ≠}, ti and tj are tuple variables, A is an attribute of the relation on which ti ranges, and B
is an attribute of the relation on which tj
ranges.
An atom of the form ti.A op c
or c op tj.B, where op is one of the compari-son operators in the set {=, <, ≤, >, ≥, ≠}, ti and tj are tuple variables, A is an attribute of the relation on which ti ranges, B
is an attribute of the relation on which tj
ranges, and c is a constant value.
Each of
the preceding atoms evaluates to either TRUE or FALSE for a specific combi-nation of
tuples; this is called the truth value
of an atom. In general, a tuple variable t
ranges over all possible tuples in
the universe. For atoms of the form R(t), if t is assigned to a tuple
that is a member of the specified
relation R, the atom is TRUE;
oth-erwise, it is FALSE. In
atoms of types 2 and 3, if the tuple variables are assigned to tuples such that
the values of the specified attributes of the tuples satisfy the condi-tion,
then the atom is TRUE.
A formula (Boolean condition) is made up
of one or more atoms connected via the logical operators AND, OR, and NOT and is
defined recursively by Rules 1 and 2 as follows:
■ Rule 1: Every atom is a formula.
Rule 2: If F1 and F2 are formulas, then so are (F1 AND F2), (F1 OR F2), NOT (F1), and NOT (F2). The truth values of
these formulas are derived from their component formulas F1 and F2
as follows:
(F1
AND F2) is TRUE if both F1 and F2 are TRUE;
otherwise, it is FALSE.
(F1
OR F2) is FALSE if both F1 and F2 are FALSE;
otherwise, it is TRUE.
NOT (F1) is TRUE if F1 is FALSE; it is FALSE if F1 is TRUE.
NOT (F2) is TRUE if F2 is FALSE; it is FALSE if F2 is TRUE.
3. The Existential and
Universal Quantifiers
In
addition, two special symbols called quantifiers
can appear in formulas; these are the universal
quantifier (∀) and the existential quantifier (∃). Truth values for formulas with
quantifiers are described in Rules 3 and 4 below; first, however, we need to
define the concepts of free and bound tuple variables in a formula. Informally,
a tuple variable t is bound if it is
quantified, meaning that it appears in an (∃t) or (∀t) clause; otherwise, it is free.
Formally, we define a tuple variable in a formula as free or bound according
to the following rules:
An occurrence of a tuple variable in a formula F that is an atom is free in F.
An occurrence of a tuple variable t is free or bound in a formula made up
of logical connectives—(F1
AND F2), (F1
OR F2), NOT(F1), and NOT(F2)— depending on whether it is free or bound in F1 or F2 (if it occurs in either). Notice that in a formula of
the form F = (F1 AND F2) or F = (F1 OR F2), a tuple variable may be free in F1 and bound in F2, or vice versa; in this
case, one occurrence of the tuple variable is bound and the other is free in F.
All free
occurrences of a tuple variable t in F are bound in a formula F of
the form F = (∃ t)(F)
or F = (∀t)(F). The tuple variable is bound to the
quanti-fier specified in F . For
example, consider the following formulas:
F1 : d.Dname=‘Research’
F2 : (∃ t)(d.Dnumber=t.Dno)
F3 : (∀d)(d.Mgr_ssn=‘333445555’)
The tuple
variable d is free in both F1 and F2, whereas it is bound to the (∀)
quan-tifier in F3.
Variable t is bound to the (∃)
quantifier in F2.
We can
now give Rules 3 and 4 for the definition of a formula we started earlier:
Rule 3: If F is a formula, then so is (∃t)(F), where t is a tuple
variable. The formula (∃t)(F) is TRUE if the
formula F evaluates to TRUE for some (at least one) tuple assigned to free occurrences of t in F;
otherwise, (∃t)(F) is FALSE.
Rule 4: If F is a formula, then so is (∀t)(F), where t is a tuple
variable. The formula (∀t)(F) is TRUE if the
formula F evaluates to TRUE for every tuple
(in the universe) assigned to free occurrences of t in F; otherwise, (∀t)(F) is FALSE.
The (∃)
quantifier is called an existential quantifier because a formula (∃t)(F) is TRUE if there
exists some
tuple that makes F
TRUE. For the
universal quantifier,
(∀t)(F) is TRUE if every
possible tuple that can be assigned to free occurrences of t in F is substituted for
t, and F is TRUE for every such substitution. It is called
the uni-versal or for all quantifier
because every tuple in the universe of
tuples must make F TRUE to make the quantified formula TRUE.
4. Sample Queries in
Tuple Relational Calculus
We will
use some of the same queries from Section 6.5 to give a flavor of how the same
queries are specified in relational algebra and in relational calculus. Notice
that some queries are easier to specify in the relational algebra than in the
relational calculus, and vice versa.
Query 1. List the name and address of all
employees who work for the ‘Research’
department.
Q1: {t.Fname, t.Lname, t.Address | EMPLOYEE(t) AND (∃d)(DEPARTMENT(d)
AND d.Dname=‘Research’ AND d.Dnumber=t.Dno)}
The only free tuple variables in a tuple
relational calculus expression should be those that appear to the left of the
bar (|). In Q1, t is the only free variable; it is then bound successively to each tuple. If a tuple satisfies the conditions specified after the bar in Q1, the
attributes Fname, Lname, and Address are retrieved for each such
tuple. The conditions
EMPLOYEE(t) and DEPARTMENT(d) specify the range relations for t and d. The condition d.Dname =
‘Research’ is a selection condition and
corresponds to a SELECT operation in the relational
algebra, whereas the condition d.Dnumber = t.Dno is a join
condition and is similar in
purpose to the (INNER) JOIN operation (see Section 6.3).
Query 2. For every project located in
‘Stafford’, list the project number, the
controlling
department number, and the department manager’s last name, birth date, and
address.
Q2: {p.Pnumber, p.Dnum, m.Lname, m.Bdate, m.Address | PROJECT(p) AND
EMPLOYEE(m) AND p.Plocation=‘Stafford’ AND ((∃d)(DEPARTMENT(d)
AND p.Dnum=d.Dnumber AND d.Mgr_ssn=m.Ssn))}
In Q2 there are two free tuple
variables, p and m. Tuple variable d is
bound to the existential quantifier. The query condition is evaluated for every
combination of tuples assigned to p
and m, and out of all possible
combinations of tuples to which p and m are bound, only the combinations that
satisfy the condition are selected.
Several
tuple variables in a query can range over the same relation. For example, to
specify Q8—for each employee, retrieve the
employee’s first and last name and the first and last name of his or her
immediate supervisor—we specify two tuple variables e and s that both range
over the EMPLOYEE
relation:
Q8: {e.Fname, e.Lname, s.Fname, s.Lname | EMPLOYEE(e) AND EMPLOYEE(s)
AND e.Super_ssn=s.Ssn}
Query 3 . List the name of each employee
who works on some
project
con-trolled by department number 5. This is a variation of Q3 in which all is changed to some.
In this case we need two join conditions and two existential quantifiers.
Q0 : {e.Lname, e.Fname | EMPLOYEE(e) AND ((∃x)(∃w)(PROJECT(x) AND
WORKS_ON(w) AND x.Dnum=5 AND w.Essn=e.Ssn
AND
x.Pnumber=w.Pno))}
Query 4. Make a list of project numbers
for projects that involve an employee
whose
last name is ‘Smith’, either as a worker or as manager of the controlling
department for the project.
Q4: { p.Pnumber | PROJECT(p) AND (((∃e)(∃w)(EMPLOYEE(e)
AND WORKS_ON(w) AND w.Pno=p.Pnumber
AND e.Lname=‘Smith’ AND e.Ssn=w.Essn) )
OR
((∃m)(∃d)(EMPLOYEE(m) AND DEPARTMENT(d)
AND p.Dnum=d.Dnumber AND d.Mgr_ssn=m.Ssn
AND m.Lname=‘Smith’)))}
Compare
this with the relational algebra version of this query in Section 6.5. The UNION operation in relational algebra
can usually be substituted with an
OR connective
in relational calculus.
5. Notation for Query
Graphs
In this
section we describe a notation that has been proposed to represent relational
calculus queries that do not involve complex quantification in a graphical
form. These types of queries are known as select-project-join
queries, because they only involve these three relational algebra
operations. The notation may be expanded to more general queries, but we do not
discuss these extensions here. This graphical representation of a query is
called a query graph. Figure 6.13
shows the query graph for Q2.
Relations in the query are represented by relation
nodes, which are dis-played as single circles. Constant values, typically
from the query selection conditions, are represented by constant nodes, which are displayed as double circles or ovals.
Selection and join conditions are represented by the graph edges (the lines that connect the nodes), as shown in Figure 6.13.
Finally, the attributes to be retrieved from each relation are displayed in
square brackets above each relation.
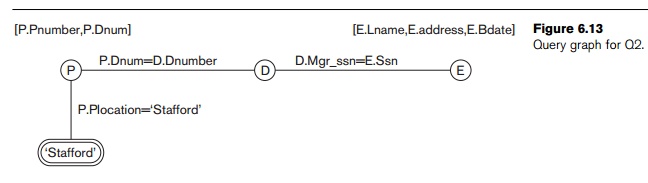
The query
graph representation does not indicate a particular order to specify which
operations to perform first, and is hence a more neutral representation of a
select-project-join query than the query tree representation (see Section
6.3.5), where the order of execution is implicitly specified. There is only a
single query graph corresponding to each query. Although some query
optimization techniques were based on query graphs, it is now generally
accepted that query trees are prefer-able because, in practice, the query
optimizer needs to show the order of operations for query execution, which is
not possible in query graphs.
In the
next section we discuss the relationship between the universal and existential
quantifiers and show how one can be transformed into the other.
6. Transforming the
Universal and Existential Quantifiers
We now
introduce some well-known transformations from mathematical logic that relate
the universal and existential quantifiers. It is possible to transform a
universal quantifier into an existential quantifier, and vice versa, to get an
equivalent expression. One general transformation can be described informally
as follows: Transform one type of quantifier into the other with negation
(preceded by NOT); AND and OR replace one another; a negated
formula becomes unnegated; and an unnegated formula becomes negated. Some
special cases of this transformation can be stated as follows, where the ≡ symbol stands for equivalent to:
(∀x) (P(x)) ≡ NOT (∃x) (NOT (P(x)))
(∃x) (P(x)) ≡ NOT (∀x) (NOT (P(x)))
(∀x) (P(x) AND Q(x)) ≡ NOT (∃x) (NOT (P(x)) OR NOT (Q(x)))
(∀x) (P(x) OR Q(x)) ≡ NOT (∃x) (NOT (P(x)) AND NOT (Q(x)))
(∃x) (P(x)) OR Q(x)) ≡ NOT (∀x) (NOT (P(x)) AND NOT (Q(x)))
(∃x) (P(x) AND Q(x)) ≡ NOT (∀x) (NOT (P(x)) OR NOT (Q(x)))
Notice
also that the following is TRUE, where
the ⇒ symbol stands for implies:
(∀x)(P(x)) ⇒ (∃x)(P(x))
NOT (∃x)(P(x)) ⇒ NOT (∀x)(P(x))
7. Using the Universal
Quantifier in Queries
Whenever
we use a universal quantifier, it is quite judicious to follow a few rules to
ensure that our expression makes sense. We discuss these rules with respect to
the query Q3.
Query 3. List the names of employees who
work on all the projects controlled by department number 5. One way
to specify this query is to use the universal quantifier as shown:
Q3: {e.Lname, e.Fname | EMPLOYEE(e) AND ((∀x)(NOT(PROJECT(x)) OR NOT (x.Dnum=5) OR ((∃w)(WORKS_ON(w) AND w.Essn=e.Ssn AND x.Pnumber=w.Pno))))}
We can
break up Q3 into its
basic components as follows:
Q3: {e.Lname, e.Fname | EMPLOYEE(e) AND F }
F =
((∀x)(NOT(PROJECT(x)) OR F1))
F1 = NOT(x.Dnum=5) OR F2
F2 = ((∃w)(WORKS_ON(w) AND w.Essn=e.Ssn
AND x.Pnumber=w.Pno))
We want
to make sure that a selected employee e
works on all the projects controlled
by department 5, but the definition of
universal quantifier says that to make the quantified formula TRUE, the inner formula must be TRUE for all tuples in the uni-verse. The
trick is to exclude from the universal quantification all tuples that we are not interested in by making the
condition TRUE for all such tuples. This is necessary
because a universally quantified tuple variable, such as x in Q3, must
evaluate to TRUE for every possible tuple assigned to it to make the
quantified formula TRUE.
The first
tuples to exclude (by making them evaluate automatically to TRUE) are those that are not in the
relation R of interest. In Q3, using the expression NOT(PROJECT(x)) inside the universally
quantified formula evaluates to TRUE all tuples x that are not in the PROJECT
relation. Then we exclude the tuples we are not interested in from R itself. In Q3, using the expression NOT(x.Dnum=5)
evaluates to TRUE all
tuples x that are in the PROJECT relation but are not controlled
by depart-ment 5. Finally, we specify a condition F2 that must hold on all the remaining tuples in R. Hence, we can explain Q3 as follows:
For the formula F = (∀x)(F) to be TRUE, we must have the formula F
be
TRUE for all
tuples in the universe that can be assigned to x.
However, in Q3 we are only interested in F being TRUE for all tuples of the PROJECT relation
that are controlled by department 5. Hence, the formula F is of the form (NOT(PROJECT(x)) OR F1). The ‘NOT (PROJECT(x)) OR ...’ condition is TRUE for all tuples not in the PROJECT relation and has the effect of eliminating these tuples from consideration in the truth value of F1. For every tuple in the PROJECT relation, F1 must be TRUE if F is to be TRUE.
Using the same line of reasoning, we do not want to
consider tuples in the PROJECT relation
that are not controlled by department number 5, since we are only interested in PROJECT tuples whose Dnum=5. Therefore, we can write:
IF (x.Dnum=5) THEN F2
which is
equivalent to
(NOT (x.Dnum=5) OR F2)
Formula F1,
hence, is of the form NOT(x.Dnum=5) OR F2. In the context of Q3, this means that, for a tuple
x in the PROJECT relation, either its Dnum≠5 or it must satisfy F2.
Finally, F2 gives the condition that
we want to hold for a selected EMPLOYEE tuple:
that the employee works on every PROJECT tuple that has not been excluded
yet. Such employee tuples are selected by the query.
In
English, Q3 gives
the following condition for selecting an EMPLOYEE tuple e: For every tuple x in the PROJECT relation
with x.Dnum=5, there must exist a tuple w
in WORKS_ON such that w.Essn=e.Ssn and w.Pno=x.Pnumber. This is
equivalent to saying
that EMPLOYEE e works on every PROJECT x in DEPARTMENT number
5. (Whew!)
Using the
general transformation from universal to existential quantifiers given in
Section 6.6.6, we can rephrase the query in Q3 as shown
in Q3A, which uses a negated
existential quantifier instead of the universal quantifier:
Q3A: {e.Lname, e.Fname | EMPLOYEE(e) AND (NOT (∃x) (PROJECT(x) AND
(x.Dnum=5) AND (NOT (∃w)(WORKS_ON(w) AND
w.Essn=e.Ssn
AND x.Pnumber=w.Pno))))}
We now
give some additional examples of queries that use quantifiers.
Query 6. List the names of employees who
have no dependents.
Q6: {e.Fname, e.Lname
| EMPLOYEE(e) AND (NOT (∃d)(DEPENDENT(d)
AND e.Ssn=d.Essn))}
Using the
general transformation rule, we can rephrase Q6 as follows:
Q6A: {e.Fname, e.Lname | EMPLOYEE(e) AND ((∀d)(NOT(DEPENDENT(d))
OR NOT(e.Ssn=d.Essn)))}
Query 7. List the names of managers who
have at least one dependent.
Q7: {e.Fname, e.Lname | EMPLOYEE(e) AND ((∃d)(∃ρ)(DEPARTMENT(d)
AND DEPENDENT(ρ) AND e.Ssn=d.Mgr_ssn AND ρ.Essn=e.Ssn))}
This
query is handled by interpreting managers
who have at least one dependent as managers
for whom there exists some dependent.
8. Safe Expressions
Whenever
we use universal quantifiers, existential quantifiers, or negation of
predicates in a calculus expression, we must make sure that the resulting
expression makes sense. A safe
expression in relational calculus is one that is guaranteed to yield a finite number of tuples as its result;
otherwise, the expression is called unsafe.
For example, the expression
{t | NOT (EMPLOYEE(t))}
is unsafe because it yields all tuples in
the universe that are not EMPLOYEE tuples, which are infinitely
numerous. If we follow the rules for Q3
discussed earlier, we will get a safe expression when using universal
quantifiers. We can define safe expressions more precisely by introducing the
concept of the domain of a tuple
relational calculus expression: This
is the set of all values that either appear as constant values in the expression or exist in any tuple
in the relations referenced in the expression. For example, the domain of {t | NOT(EMPLOYEE(t))} is the set of all attribute values appearing in some tuple of
the EMPLOYEE relation (for any attribute).
The domain of the expression Q3A would
include all values appearing in EMPLOYEE, PROJECT, and WORKS_ON (unioned with the value 5
appearing in the query itself).
An
expression is said to be safe if all
values in its result are from the domain of the expression. Notice that the
result of {t | NOT(EMPLOYEE(t))} is
unsafe, since it will, in general, include tuples (and hence values) from
outside the EMPLOYEE
relation; such values are not in the domain of the expression. All of our other
examples are safe expressions.
Related Topics