Relational Algebra Operations from Set Theory

Relational Algebra Operations from Set Theory

1. The UNION, INTERSECTION, and MINUS Operations

The next group of relational algebra operations are the standard mathematical operations on sets. For example, to retrieve the Social Security numbers of all employees who either work in department 5 or directly supervise an employee who works in department 5, we can use the UNION operation as follows:

DEP5_EMPS ← σ_Dno=5(EMPLOYEE)

RESULT1 ← π_Ssn(DEP5_EMPS)

RESULT2(Ssn) ← π_{Super_ssn}(DEP5_EMPS)

RESULT ← RESULT1 ∪ RESULT2

The relation RESULT1 has the Ssn of all employees who work in department 5, whereas RESULT2 has the Ssn of all employees who directly supervise an employee who works in department 5. The UNION operation produces the tuples that are in either RESULT1 or RESULT2 or both (see Figure 6.3), while eliminating any duplicates. Thus, the Ssn value ‘333445555’ appears only once in the result.

Several set theoretic operations are used to merge the elements of two sets in various ways, including UNION, INTERSECTION, and SET DIFFERENCE (also called MINUS or EXCEPT). These are binary operations; that is, each is applied to two sets (of tuples). When these operations are adapted to relational databases, the two relations on which any of these three operations are applied must have the same type of tuples; this condition has been called union compatibility or type compatibility. Two relations R(A₁, A₂, ..., A_n) and S(B₁, B₂, ..., B_n) are said to be union compatible (or type compatible) if they have the same degree n and if dom(A_i) = dom(B_i) for 1 f i f n. This means that the two relations have the same number of attributes and each corresponding pair of attributes has the same domain.

We can define the three operations UNION, INTERSECTION, and SET DIFFERENCE on two union-compatible relations R and S as follows:

■      UNION: The result of this operation, denoted by R ∪ S, is a relation that includes all tuples that are either in R or in S or in both R and S. Duplicate tuples are eliminated.

■      INTERSECTION: The result of this operation, denoted by R ∩ S, is a relation that includes all tuples that are in both R and S.

■      SET DIFFERENCE (or MINUS): The result of this operation, denoted by R – S, is a relation that includes all tuples that are in R but not in S.

We will adopt the convention that the resulting relation has the same attribute names as the first relation R. It is always possible to rename the attributes in the result using the rename operator.

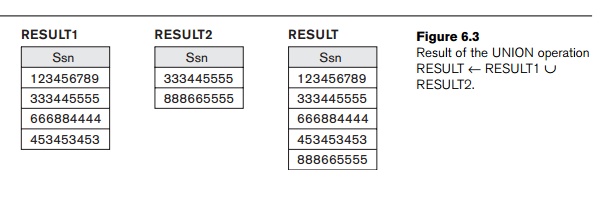
Figure 6.4 illustrates the three operations. The relations STUDENT and INSTRUCTOR in Figure 6.4(a) are union compatible and their tuples represent the names of students and the names of instructors, respectively. The result of the UNION operation in Figure 6.4(b) shows the names of all students and instructors. Note that duplicate tuples appear only once in the result. The result of the INTERSECTION operation (Figure 6.4(c)) includes only those who are both students and instructors.

Notice that both UNION and INTERSECTION are commutative operations; that is,

R ∪ S = S ∪ R                          and R ∩ S = S ∩ R

Both UNION and INTERSECTION can be treated as n-ary operations applicable to any number of relations because both are also associative operations; that is,

R ∪ (S ∪ T ) = (R ∪ S ) ∪ T                     and (R ∩ S ) ∩ T = R ∩ (S ∩ T )

The MINUS operation is not commutative; that is, in general,

R − S ≠ S − R

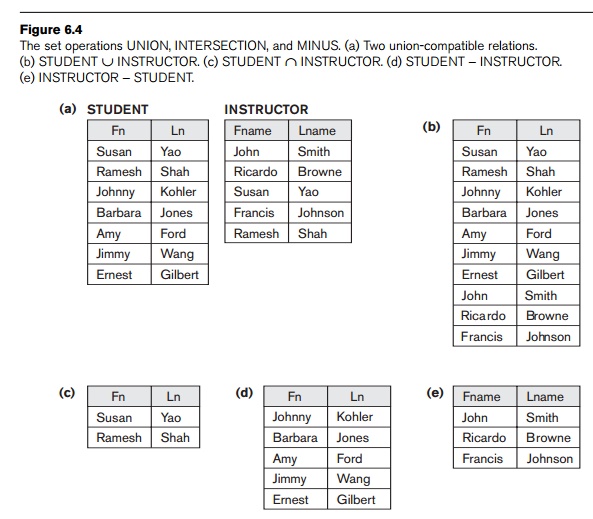
Figure 6.4(d) shows the names of students who are not instructors, and Figure 6.4(e) shows the names of instructors who are not students.

Note that INTERSECTION can be expressed in terms of union and set difference as follows:

R ∩ S = ((R ∪ S ) − (R − S )) − (S − R )

In SQL, there are three operations—UNION, INTERSECT, and EXCEPT—that correspond to the set operations described here. In addition, there are multiset operations (UNION ALL, INTERSECT ALL, and EXCEPT ALL) that do not eliminate duplicates (see Section 4.3.4).

2. The CARTESIAN PRODUCT (CROSS PRODUCT) Operation

Next, we discuss the CARTESIAN PRODUCT operation—also known as CROSS PRODUCT or CROSS JOIN—which is denoted by ×. This is also a binary set operation, but the relations on which it is applied do not have to be union compatible. In its binary form, this set operation produces a new element by combining every member (tuple) from one relation (set) with every member (tuple) from the other relation (set). In general, the result of R(A₁, A₂, ..., A_n) × S(B₁, B₂, ..., B_m) is a relation Q with degree n + m attributes Q(A₁, A₂, ..., A_n, B₁, B₂, ..., B_m), in that order. The resulting relation Q has one tuple for each combination of tuples—one from R and one from S. Hence, if R has n_R tuples (denoted as |R| = n_R), and S has n_S tuples, then R × S will have n_{R *} n_S tuples.

The n-ary CARTESIAN PRODUCT operation is an extension of the above concept, which produces new tuples by concatenating all possible combinations of tuples from n underlying relations.

In general, the CARTESIAN PRODUCT operation applied by itself is generally mean-ingless. It is mostly useful when followed by a selection that matches values of attributes coming from the component relations. For example, suppose that we want to retrieve a list of names of each female employee’s dependents. We can do this as follows:

FEMALE_EMPS ← σ_Sex=‘F’(EMPLOYEE)

EMPNAMES ← π_{Fname, Lname, Ssn}(FEMALE_EMPS)

EMP_DEPENDENTS ← EMPNAMES × DEPENDENT

ACTUAL_DEPENDENTS ← σ_Ssn=Essn(EMP_DEPENDENTS)

RESULT ← π_{Fname, Lname, Dependent_name}(ACTUAL_DEPENDENTS)

The resulting relations from this sequence of operations are shown in Figure 6.5. The EMP_DEPENDENTS relation is the result of applying the CARTESIAN PROD-UCT operation to EMPNAMES from Figure 6.5 with DEPENDENT from Figure 3.6. In EMP_DEPENDENTS, every tuple from EMPNAMES is combined with every tuple from DEPENDENT, giving a result that is not very meaningful (every dependent is combined with every female employee). We want to combine a female employee tuple only with her particular dependents—namely, the DEPENDENT tuples whose

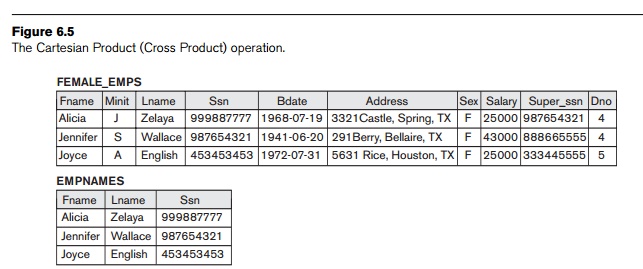
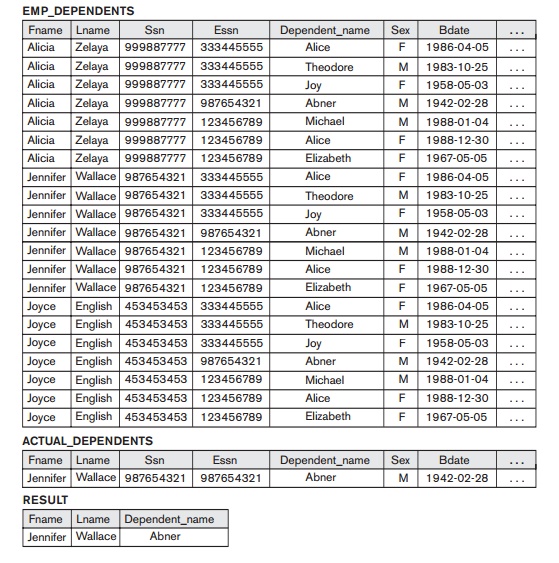
Essn value match the Ssn value of the EMPLOYEE tuple. The ACTUAL_DEPENDENTS relation accomplishes this. The EMP_DEPENDENTS relation is a good example of the case where relational algebra can be correctly applied to yield results that make no sense at all. It is the responsibility of the user to make sure to apply only meaningful operations to relations.

The CARTESIAN PRODUCT creates tuples with the combined attributes of two relations. We can SELECT related tuples only from the two relations by specifying an appropriate selection condition after the Cartesian product, as we did in the preceding example. Because this sequence of CARTESIAN PRODUCT followed by SELECT is quite commonly used to combine related tuples from two relations, a special operation, called JOIN, was created to specify this sequence as a single operation. We dis-cuss the JOIN operation next.

In SQL, CARTESIAN PRODUCT can be realized by using the CROSS JOIN option in joined tables (see Section 5.1.6). Alternatively, if there are two tables in the WHERE clause and there is no corresponding join condition in the query, the result will also be the CARTESIAN PRODUCT of the two tables (see Q10 in Section 4.3.3).