Additional Relational Operations

Additional Relational Operations

Some common database requests—which are needed in commercial applications for RDBMSs—cannot be performed with the original relational algebra operations described in Sections 6.1 through 6.3. In this section we define additional operations to express these requests. These operations enhance the expressive power of the original relational algebra.

1. Generalized Projection

The generalized projection operation extends the projection operation by allowing functions of attributes to be included in the projection list. The generalized form can be expressed as:

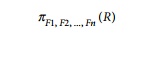
where F₁, F₂, ..., F_n are functions over the attributes in relation R and may involve arithmetic operations and constant values. This operation is helpful when develop-ing reports where computed values have to be produced in the columns of a query result.

As an example, consider the relation

EMPLOYEE (Ssn, Salary, Deduction, Years_service)

A report may be required to show

Net Salary = Salary – Deduction,

Bonus = 2000 _* Years_service, and

Tax = 0.25 _* Salary.

Then a generalized projection combined with renaming may be used as follows:

^{REPORT ← ρ}(Ssn, Net_salary, Bonus, Tax)^(πSsn, Salary – Deduction, 2000 _* Years_service,

                                                                               _{* Salary}(EMPLOYEE)).

2. Aggregate Functions and Grouping

Another type of request that cannot be expressed in the basic relational algebra is to specify mathematical aggregate functions on collections of values from the data-base. Examples of such functions include retrieving the average or total salary of all employees or the total number of employee tuples. These functions are used in simple statistical queries that summarize information from the database tuples. Common functions applied to collections of numeric values include SUM, AVERAGE, MAXIMUM, and MINIMUM. The COUNT function is used for counting tuples or values.

Another common type of request involves grouping the tuples in a relation by the value of some of their attributes and then applying an aggregate function independently to each group. An example would be to group EMPLOYEE tuples by Dno, so that each group includes the tuples for employees working in the same department. We can then list each Dno value along with, say, the average salary of employees within the department, or the number of employees who work in the department.

We can define an AGGREGATE FUNCTION operation, using the symbol ℑ (pronounced script F)⁷, to specify these types of requests as follows:

<grouping attributes> ^ℑ <function list> ^(R)

where <grouping attributes> is a list of attributes of the relation specified in R, and <function list> is a list of (<function> <attribute>) pairs. In each such pair, <function> is one of the allowed functions—such as SUM, AVERAGE, MAXIMUM, MINIMUM, COUNT—and <attribute> is an attribute of the relation specified by R. The resulting relation has the grouping attributes plus one attribute for each element in the function list. For example, to retrieve each department number, the number of employees in the department, and their average salary, while renaming the resulting attributes as indicated below, we write:

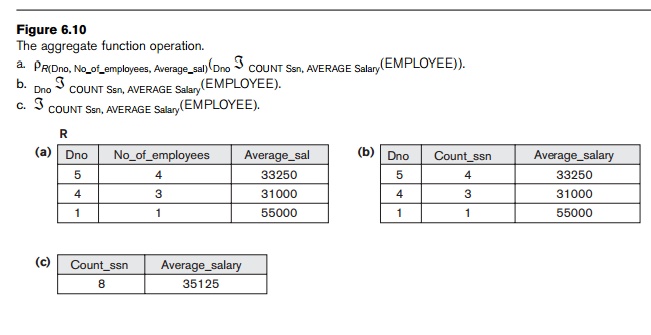
^ρR(Dno, No_of_employees, Average_sal)⁽Dno ^ℑ COUNT Ssn, AVERAGE Salary ^(EMPLOYEE))

The result of this operation on the EMPLOYEE relation of Figure 3.6 is shown in Figure 6.10(a).

In the above example, we specified a list of attribute names—between parentheses in the RENAME operation—for the resulting relation R. If no renaming is applied, then the attributes of the resulting relation that correspond to the function list will each be the concatenation of the function name with the attribute name in the form <function>_<attribute>.⁸ For example, Figure 6.10(b) shows the result of the fol-lowing operation:

Dno ^ℑ COUNT Ssn, AVERAGE Salary^(EMPLOYEE)

If no grouping attributes are specified, the functions are applied to all the tuples in the relation, so the resulting relation has a single tuple only. For example, Figure 6.10(c) shows the result of the following operation:

^ℑ COUNT Ssn, AVERAGE Salary^(EMPLOYEE)

It is important to note that, in general, duplicates are not eliminated when an aggregate function is applied; this way, the normal interpretation of functions such as

SUM and AVERAGE is computed. It is worth emphasizing that the result of applying an aggregate function is a relation, not a scalar number—even if it has a single value. This makes the relational algebra a closed mathematical system.

3. Recursive Closure Operations

Another type of operation that, in general, cannot be specified in the basic original relational algebra is recursive closure. This operation is applied to a recursive relationship between tuples of the same type, such as the relationship between an employee and a supervisor. This relationship is described by the foreign key Super_ssn of the EMPLOYEE relation in Figures 3.5 and 3.6, and it relates each employee tuple (in the role of supervisee) to another employee tuple (in the role of supervisor). An example of a recursive operation is to retrieve all supervisees of an employee e at all levels—that is, all employees e directly supervised by e, all employees e ℑ directly supervised by each employee e , all employees e directly supervised by each employee e , and so on.

It is relatively straightforward in the relational algebra to specify all employees supervised by e at a specific level by joining the table with itself one or more times. However, it is difficult to specify all supervisees at all levels. For example, to specify the Ssns of all employees e directly supervised—at level one—by the employee e whose name is ‘James Borg’ (see Figure 3.6), we can apply the following operation:

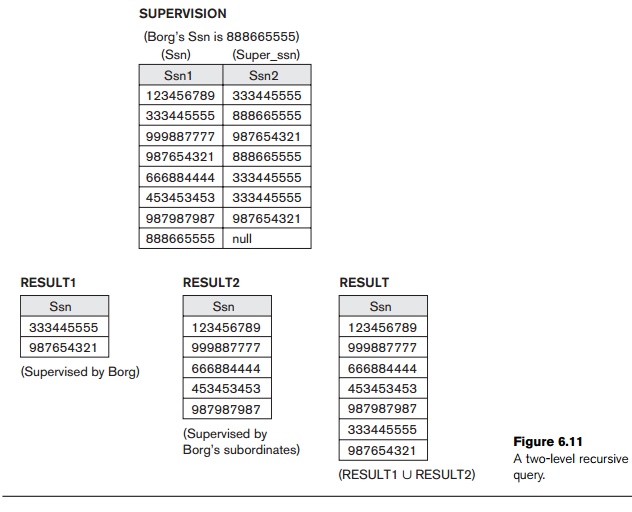
^{BORG_SSN ← π}Ssn^(σFname=‘James’ AND Lname=‘Borg’^(EMPLOYEE))

SUPERVISION(Ssn1, Ssn2) ← π_{Ssn,Super_ssn}(EMPLOYEE)

RESULT1(Ssn) ← π_Ssn1(SUPERVISION  _Ssn2=SsnBORG_SSN)

To retrieve all employees supervised by Borg at level 2—that is, all employees e supervised by some employee e who is directly supervised by Borg—we can apply another JOIN to the result of the first query, as follows:

RESULT2(Ssn) ← π_Ssn1(SUPERVISION   _Ssn2=SsnRESULT1)

To get both sets of employees supervised at levels 1 and 2 by ‘James Borg’, we can apply the UNION operation to the two results, as follows:

RESULT ← RESULT2 ∪ RESULT1

The results of these queries are illustrated in Figure 6.11. Although it is possible to retrieve employees at each level and then take their UNION, we cannot, in general, specify a query such as “retrieve the supervisees of ‘James Borg’ at all levels” without utilizing a looping mechanism unless we know the maximum number of levels. An operation called the transitive closure of relations has been proposed to compute the recursive relationship as far as the recursion proceeds.

4. OUTER JOIN Operations

Next, we discuss some additional extensions to the JOIN operation that are necessary to specify certain types of queries. The JOIN operations described earlier match tuples that satisfy the join condition. For example, for a NATURAL JOIN operation R _* S, only tuples from R that have matching tuples in S—and vice versa—appear in the result. Hence, tuples without a matching (or related) tuple are eliminated from the JOIN result. Tuples with NULL values in the join attributes are also eliminated. This type of join, where tuples with no match are eliminated, is known as an inner join. The join operations we described earlier in Section 6.3 are all inner joins. This amounts to the loss of information if the user wants the result of the JOIN to include all the tuples in one or more of the component relations.

A set of operations, called outer joins, were developed for the case where the user wants to keep all the tuples in R, or all those in S, or all those in both relations in the result of the JOIN, regardless of whether or not they have matching tuples in the other relation. This satisfies the need of queries in which tuples from two tables are to be combined by matching corresponding rows, but without losing any tuples for lack of matching values. For example, suppose that we want a list of all employee names as well as the name of the departments they manage if they happen to manage a department; if they do not manage one, we can indicate it with a NULL value. We can apply an operation LEFT OUTER JOIN, denoted by  , to retrieve the result as follows:

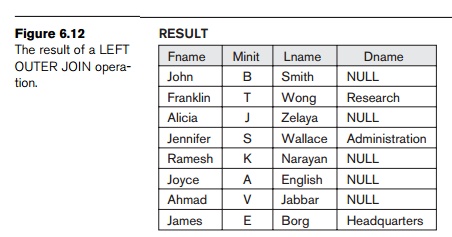
TEMP ← (EMPLOYEE  _{Ssn=Mgr_ssn}DEPARTMENT)

^{RESULT ← π}Fname, Minit, Lname, Dname^(TEMP)

The LEFT OUTER JOIN operation keeps every tuple in the first, or left, relation R in R  S; if no matching tuple is found in S, then the attributes of S in the join result are filled or padded with NULL values. The result of these operations is shown in Figure 6.12.

A similar operation, RIGHT OUTER JOIN, denoted by  , keeps every tuple in the second, or right, relation S in the result of R  S. A third operation, FULL OUTER JOIN, denoted by   , keeps all tuples in both the left and the right relations when no matching tuples are found, padding them with NULL values as needed. The three outer join operations are part of the SQL2 standard (see Section 5.1.6). These operations were provided later as an extension of relational algebra in response to the typical need in business applications to show related information from multiple tables exhaustively. Sometimes a complete reporting of data from multiple tables is required whether or not there are matching values.

5. The OUTER UNION Operation

The OUTER UNION operation was developed to take the union of tuples from two relations that have some common attributes, but are not union (type) compatible. This operation will take the UNION of tuples in two relations R(X, Y ) and S(X, Z) that are partially compatible, meaning that only some of their attributes, say X, are union compatible. The attributes that are union compatible are represented only once in the result, and those attributes that are not union compatible from either

relation are also kept in the result relation T(X, Y, Z). It is therefore the same as a FULL OUTER JOIN on the common attributes.

Two tuples t₁ in R and t₂ in S are said to match if t₁[X]=t₂[X]. These will be combined (unioned) into a single tuple in t. Tuples in either relation that have no matching tuple in the other relation are padded with NULL values. For example, an OUTER UNION can be applied to two relations whose schemas are STUDENT(Name,

Ssn, Department, Advisor) and INSTRUCTOR(Name, Ssn, Department, Rank). Tuples from the two relations are matched based on having the same combination of values of the shared attributes—Name, Ssn, Department. The resulting relation, STUDENT_OR_INSTRUCTOR, will have the following attributes:

STUDENT_OR_INSTRUCTOR(Name, Ssn, Department, Advisor, Rank)

All the tuples from both relations are included in the result, but tuples with the same (Name, Ssn, Department) combination will appear only once in the result. Tuples appearing only in STUDENT will have a NULL for the Rank attribute, whereas tuples appearing only in INSTRUCTOR will have a NULL for the Advisor attribute. A tuple that exists in both relations, which represent a student who is also an instructor, will have values for all its attributes.

Notice that the same person may still appear twice in the result. For example, we could have a graduate student in the Mathematics department who is an instructor in the Computer Science department. Although the two tuples representing that person in STUDENT and INSTRUCTOR will have the same (Name, Ssn) values, they will not agree on the Department value, and so will not be matched. This is because Department has two different meanings in STUDENT (the department where the per-son studies) and INSTRUCTOR (the department where the person is employed as an instructor). If we wanted to apply the OUTER UNION based on the same (Name, Ssn) combination only, we should rename the Department attribute in each table to reflect that they have different meanings and designate them as not being part of the union-compatible attributes. For example, we could rename the attributes as MajorDept in STUDENT and WorkDept in INSTRUCTOR.