Binary Relational Operations: JOIN and DIVISION

Binary Relational Operations: JOIN and DIVISION

1. The JOIN Operation

The JOIN operation, denoted by  , is used to combine related tuples from two rela-tions into single “longer” tuples. This operation is very important for any relational database with more than a single relation because it allows us to process relation-ships among relations. To illustrate JOIN, suppose that we want to retrieve the name of the manager of each department. To get the manager’s name, we need to combine each department tuple with the employee tuple whose Ssn value matches the Mgr_ssn value in the department tuple. We do this by using the JOIN operation and then projecting the result over the necessary attributes, as follows:

DEPT_MGR ← DEPARTMENT  _{Mgr_ssn=Ssn} EMPLOYEE

RESULT ← π_{Dname, Lname, Fname}(DEPT_MGR)

The first operation is illustrated in Figure 6.6. Note that Mgr_ssn is a foreign key of the DEPARTMENT relation that references Ssn, the primary key of the EMPLOYEE relation. This referential integrity constraint plays a role in having matching tuples in the referenced relation EMPLOYEE.

The JOIN operation can be specified as a CARTESIAN PRODUCT operation followed by a SELECT operation. However, JOIN is very important because it is used very frequently when specifying database queries. Consider the earlier example illustrating CARTESIAN PRODUCT, which included the following sequence of operations:

EMP_DEPENDENTS ← EMPNAMES × DEPENDENT

ACTUAL_DEPENDENTS ← σ_Ssn=Essn(EMP_DEPENDENTS)

These two operations can be replaced with a single JOIN operation as follows:

The result of the JOIN is a relation Q with n + m attributes Q(A₁, A₂, ..., A_n, B₁, B₂, ... , B_m) in that order; Q has one tuple for each combination of tuples—one from R and one from S—whenever the combination satisfies the join condition. This is the main difference between CARTESIAN PRODUCT and JOIN. In JOIN, only combina-tions of tuples satisfying the join condition appear in the result, whereas in the CARTESIAN PRODUCT all combinations of tuples are included in the result. The join condition is specified on attributes from the two relations R and S and is evaluated for each combination of tuples. Each tuple combination for which the join condition evaluates to TRUE is included in the resulting relation Q as a single combined tuple.

A general join condition is of the form

<condition> AND <condition> AND...AND <condition>

where each <condition> is of the form A_i θ B_j, A_i is an attribute of R, B_j is an attribute of S, A_i and B_j have the same domain, and θ (theta) is one of the comparison operators {=, <, ≤, >, ≥, ≠}. A JOIN operation with such a general join condition is called a THETA JOIN. Tuples whose join attributes are NULL or for which the join condition is FALSE do not appear in the result. In that sense, the JOIN operation does not necessarily preserve all of the information in the participating relations, because tuples that do not get combined with matching ones in the other relation do not appear in the result.

2. Variations of JOIN: The EQUIJOIN and NATURAL JOIN

The most common use of JOIN involves join conditions with equality comparisons only. Such a JOIN, where the only comparison operator used is =, is called an EQUIJOIN. Both previous examples were EQUIJOINs. Notice that in the result of an EQUIJOIN we always have one or more pairs of attributes that have identical values in every tuple. For example, in Figure 6.6, the values of the attributes Mgr_ssn and Ssn are identical in every tuple of DEPT_MGR (the EQUIJOIN result) because the equality join condition specified on these two attributes requires the values to be identical in every tuple in the result. Because one of each pair of attributes with identical values is superfluous, a new operation called NATURAL JOIN—denoted by _* —was created to get rid of the second (superfluous) attribute in an EQUIJOIN condition. The standard definition of NATURAL JOIN requires that the two join attributes (or each pair of join attributes) have the same name in both relations. If this is not the case, a renaming operation is applied first.

Suppose we want to combine each PROJECT tuple with the DEPARTMENT tuple that controls the project. In the following example, first we rename the Dnumber attribute of DEPARTMENT to Dnum—so that it has the same name as the Dnum attribute in

PROJECT—and then we apply NATURAL JOIN:

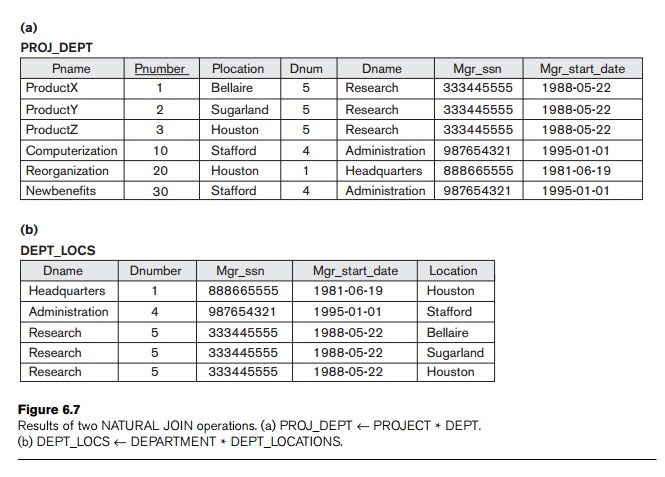
^{PROJ_DEPT ← PROJECT} * ^ρ_{(Dname, Dnum, Mgr_ssn, Mgr_start_date)}^(DEPARTMENT)

The same query can be done in two steps by creating an intermediate table DEPT as follows:

^{DEPT ← ρ}(Dname, Dnum, Mgr_ssn, Mgr_start_date)^(DEPARTMENT)

PROJ_DEPT ← PROJECT _* DEPT

The attribute Dnum is called the join attribute for the NATURAL JOIN operation, because it is the only attribute with the same name in both relations. The resulting relation is illustrated in Figure 6.7(a). In the PROJ_DEPT relation, each tuple combines a PROJECT tuple with the DEPARTMENT tuple for the department that controls the project, but only one join attribute value is kept.

If the attributes on which the natural join is specified already have the same names in both relations, renaming is unnecessary. For example, to apply a natural join on the Dnumber attributes of DEPARTMENT and DEPT_LOCATIONS, it is sufficient to write

DEPT_LOCS ← DEPARTMENT _* DEPT_LOCATIONS

The resulting relation is shown in Figure 6.7(b), which combines each department with its locations and has one tuple for each location. In general, the join condition for NATURAL JOIN is constructed by equating each pair of join attributes that have the same name in the two relations and combining these conditions with AND. There can be a list of join attributes from each relation, and each corresponding pair must have the same name.

A more general, but nonstandard definition for NATURAL JOIN is

^{Q ← R} *(<list1>),(<list2>)^S

In this case, <list1> specifies a list of i attributes from R, and <list2> specifies a list of i attributes from S. The lists are used to form equality comparison conditions between pairs of corresponding attributes, and the conditions are then ANDed together. Only the list corresponding to attributes of the first relation R—<list1>— is kept in the result Q.

Notice that if no combination of tuples satisfies the join condition, the result of a JOIN is an empty relation with zero tuples. In general, if R has n_R tuples and S has n_S

tuples, the result of a JOIN operation R_{<join condition>} S will have between zero and n_{R *} n_S tuples. The expected size of the join result divided by the maximum size n_{R *}

n_S leads to a ratio called join selectivity, which is a property of each join condition. If there is no join condition, all combinations of tuples qualify and the JOIN degen-erates into a CARTESIAN PRODUCT, also called CROSS PRODUCT or CROSS JOIN.

As we can see, a single JOIN operation is used to combine data from two relations so that related information can be presented in a single table. These operations are also known as inner joins, to distinguish them from a different join variation called outer joins (see Section 6.4.4). Informally, an inner join is a type of match and com-bine operation defined formally as a combination of CARTESIAN PRODUCT and SELECTION. Note that sometimes a join may be specified between a relation and itself, as we will illustrate in Section 6.4.3. The NATURAL JOIN or EQUIJOIN opera-tion can also be specified among multiple tables, leading to an n-way join. For example, consider the following three-way join:

((PROJECT _Dnum=DnumberDEPARTMENT)_{Mgr_ssn=Ssn}EMPLOYEE)

This combines each project tuple with its controlling department tuple into a single tuple, and then combines that tuple with an employee tuple that is the department manager. The net result is a consolidated relation in which each tuple contains this project-department-manager combined information.

In SQL, JOIN can be realized in several different ways. The first method is to specify the <join conditions> in the WHERE clause, along with any other selection conditions. This is very common, and is illustrated by queries Q1, Q1A, Q1B, Q2, and Q8 in Sections 4.3.1 and 4.3.2, as well as by many other query examples in Chapters 4 and 5. The second way is to use a nested relation, as illustrated by queries Q4A and Q16 in Section 5.1.2. Another way is to use the concept of joined tables, as illustrated by the queries Q1A, Q1B, Q8B, and Q2A in Section 5.1.6. The construct of joined tables was added to SQL2 to allow the user to specify explicitly all the various types of joins, because the other methods were more limited. It also allows the user to clearly distinguish join conditions from the selection conditions in the WHERE clause.

3. A Complete Set of Relational Algebra Operations

It has been shown that the set of relational algebra operations {σ, π, ∪, ρ, –, ×} is a complete set; that is, any of the other original relational algebra operations can be expressed as a sequence of operations from this set. For example, the INTERSECTION operation can be expressed by using UNION and MINUS as follows:

R ∩ S ≡ (R ∪ S) – ((R – S) ∪ (S – R))

Although, strictly speaking, INTERSECTION is not required, it is inconvenient to specify this complex expression every time we wish to specify an intersection. As another example, a JOIN operation can be specified as a CARTESIAN PRODUCT fol-lowed by a SELECT operation, as we discussed:

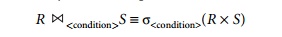
Similarly, a NATURAL JOIN can be specified as a CARTESIAN PRODUCT preceded by RENAME and followed by SELECT and PROJECT operations. Hence, the various JOIN operations are also not strictly necessary for the expressive power of the rela-tional algebra. However, they are important to include as separate operations because they are convenient to use and are very commonly applied in database applications. Other operations have been included in the basic relational algebra for convenience rather than necessity. We discuss one of these—the DIVISION operation—in the next section.

4. The DIVISION Operation

The DIVISION operation, denoted by ÷, is useful for a special kind of query that sometimes occurs in database applications. An example is Retrieve the names of employees who work on all the projects that ‘John Smith’ works on. To express this query using the DIVISION operation, proceed as follows. First, retrieve the list of project numbers that ‘John Smith’ works on in the intermediate relation

SMITH_PNOS:

^{SMITH ← σ}Fname=‘John’ AND Lname=‘Smith’^(EMPLOYEE)

SMITH_PNOS ← π_Pno(WORKS_ON_Essn=SsnSMITH)

Next, create a relation that includes a tuple <Pno, Essn> whenever the employee whose Ssn is Essn works on the project whose number is Pno in the intermediate relation SSN_PNOS:

SSN_PNOS ← π_{Essn, Pno}(WORKS_ON)

Finally, apply the DIVISION operation to the two relations, which gives the desired employees’ Social Security numbers:

SSNS(Ssn) ← SSN_PNOS ÷ SMITH_PNOS

^{RESULT ← π}_{Fname, Lname}^(SSNS * ^EMPLOYEE)

The preceding operations are shown in Figure 6.8(a)

In general, the DIVISION operation is applied to two relations R(Z) ÷ S(X), where the attributes of R are a subset of the attributes of S; that is, X ⊆ Z. Let Y be the set of attributes of R that are not attributes of S; that is, Y = Z – X (and hence Z = X ∪ Y ). The result of DIVISION is a relation T(Y) that includes a tuple t if tuples t_R appear in R with t_R [Y] = t, and with t_R [X] = t_S for every tuple t_S in S. This means that, for a tuple t to appear in the result T of the DIVISION, the values in t must appear in R in combination with every tuple in S. Note that in the formulation of the DIVISION operation, the tuples in the denominator relation S restrict the numerator relation R by selecting those tuples in the result that match all values present in the denomina-tor. It is not necessary to know what those values are as they can be computed by another operation, as illustrated in the SMITH_PNOS relation in the above example.

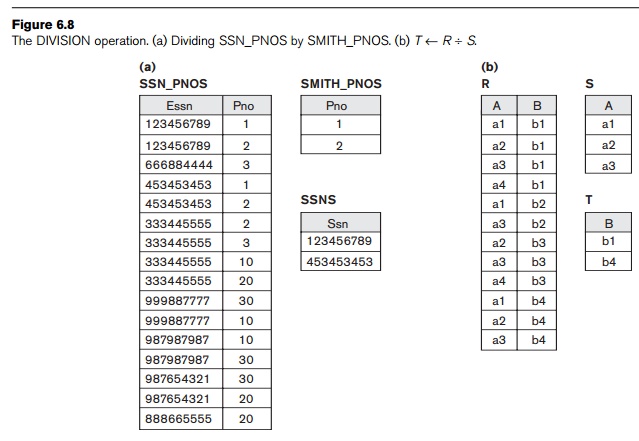
Figure 6.8(b) illustrates a DIVISION operation where X = {A}, Y = {B}, and Z = {A, B}. Notice that the tuples (values) b₁ and b₄ appear in R in combination with all three tuples in S; that is why they appear in the resulting relation T. All other values of B in R do not appear with all the tuples in S and are not selected: b₂ does not appear with a₂, and b₃ does not appear with a₁.

The DIVISION operation can be expressed as a sequence of π, ×, and – operations as follows:

T1 ← π_Y(R)

T2 ← π_Y((S × T1) – R)

T ← T1 – T2

The DIVISION operation is defined for convenience for dealing with queries that involve universal quantification (see Section 6.6.7) or the all condition. Most RDBMS implementations with SQL as the primary query language do not directly implement division. SQL has a roundabout way of dealing with the type of query illustrated above (see Section 5.1.4, queries Q3A and Q3B). Table 6.1 lists the various basic relational algebra operations we have discussed.

5. Notation for Query Trees

In this section we describe a notation typically used in relational systems to represent queries internally. The notation is called a query tree or sometimes it is known as a query evaluation tree or query execution tree. It includes the relational algebra operations being executed and is used as a possible data structure for the internal representation of the query in an RDBMS.

A query tree is a tree data structure that corresponds to a relational algebra expression. It represents the input relations of the query as leaf nodes of the tree, and rep-resents the relational algebra operations as internal nodes. An execution of the query tree consists of executing an internal node operation whenever its operands (represented by its child nodes) are available, and then replacing that internal node by the relation that results from executing the operation. The execution terminates when the root node is executed and produces the result relation for the query.

^πPnumber, Dnum, Lname, Address, Bdate^(((σPlocation=‘Stafford’^(PROJECT))

_Dnum=Dnumber(DEPARTMENT))_{Mgr_ssn=Ssn}(EMPLOYEE))

In Figure 6.9, the three leaf nodes P, D, and E represent the three relations PROJECT, DEPARTMENT, and EMPLOYEE. The relational algebra operations in the expression

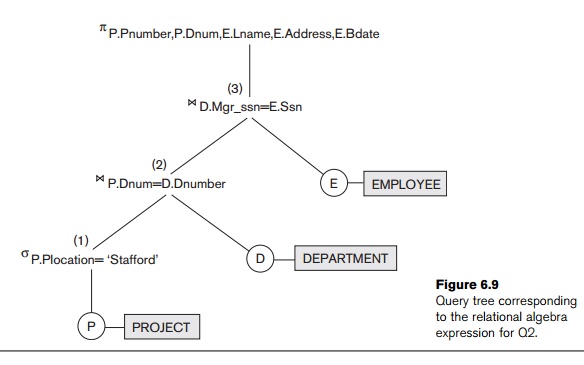
are represented by internal tree nodes. The query tree signifies an explicit order of execution in the following sense. In order to execute Q2, the node marked (1) in Figure 6.9 must begin execution before node (2) because some resulting tuples of operation (1) must be available before we can begin to execute operation (2). Similarly, node (2) must begin to execute and produce results before node (3) can start execution, and so on. In general, a query tree gives a good visual representation and understanding of the query in terms of the relational operations it uses and is recommended as an additional means for expressing queries in relational algebra. We will revisit query trees when we discuss query processing and optimization in Chapter 19.