The Distortion Less Line

THE DISTORTION LESS LINE

It is desirable, however to know the condition on the line parameters that allows propagation without distortion. The line having parameters satisfy this condition is termed as a distortion less line.

The condition for a distortion less line was first investigated by Oliver Heaviside. Distortion less condition can help in designing new lines or modifying old ones to minimize distortion.

A line, which has neither frequency distortion nor phase distortion is called a distortion less line.

Condition for a distortion less line

The condition for a distortion less line is RC=LG. Also,

a)The attenuation constant _ should be made independent of frequency. α = RG

b) The phase constant _ should be made dependent of frequency. β = ω LC

c) The velocity of propagation is independent of frequency.

V=1 / LC

For the telephone cable to be distortion less line, the inductance value should be increased by placing lumped inductors along the line.

For a perfect line, the resistance and the leakage conductance value were neglected. The conditions for a perfect line are R=G=0. Smooth line is one in which the load is terminated by its characteristic impedance and no reflections occur in such a line. It is also called as flat line.

The distortion Less Iine

If a line is to have neither frequency nor delay distortion, then attenuation constant and velocity of propagation cannot be function of frequency.

Then the phase constant be a direct fuction of frequency

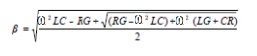
The above equation shows that if the the term under the second radical be reduced to equal

(RG + ω2LC)2

Then the required condition for ß is obtained. Expanding the term under the internal radical and forcing the equality gives

R2G2- 2 ω2LCRG+  ω4L2C2+  ω2L2G2+ 2 ω2LCRG+  ω2CR2 = (RG+ ω2LC)2

This reduces to

2 ω2LCRG+  ω2L2G2+  ω2CR2=0

(LG-CR)2=0

Therefore the condition that will make phase constant a direct form is

LG = CR

A hypothetical line might be built to fulfill this condition. The line would then have a value of ß obtained by use of the above equation.

Already we know that the formula for the phase constant

β =  ωLC

Then the velocity of propagation will be v = 1/ LC

This is the same for the all frequencies, thus eliminating the delay distortion.

May be made independent of frequency if the term under the internal radical is forced to reduce to (RG +ω LC)2

Analysis shows that the condition for the distortion less line LG = CR , will produce the desired result, so that it is possible to make attenuation constant and velocity independent of frequency simultaneously. Applying the condition LG= RC to the expression for the attenuation gives α = RG

This is the independent of frequency, thus eliminating frequency distortion on a line. To achieve

LG = CR

Require a very large value of L, since G is small. If G is intentionally increased, attenuation are increased, resulting in poor line efficiency.

To reduce R raises the size and cost of the conductors above economic limits, so that the hypothetical results cannot be achieved.

Propagation constant is as the natural logarithm of the ratio of the sending end current or voltage to the receiving end current or voltage of the line. It gives the manner in the wave is propagated along a line and specifies the variation of voltage and current in the line as a function of distance. Propagation constant is a complex quantity and is expressed as γ= α + j β.

The real part is called the attenuation constant, whereas the imaginary part of propagation constant is called the phase constant.