Chapter: Transmission Lines and Waveguides : Transmission Line Theory
Calculation of Current, Voltage, Power Delivered and Efficiency of Transmission
CALCULATION OF CURRENT, VOLTAGE, POWER DELIVERED AND EFFICIENCY OF TRANSMISSION
Voltage and Current ratios
In order to simplify calculations, sinusoidal voltage and current waves are commonly represented as complex-valued functions of time denoted as v and I
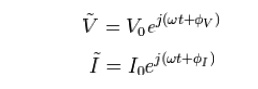
Impedance is defined as the ratio of these quantities

Substituting these into Ohm's law we have

Noting that this must hold for all t, we may equate the magnitudes and phases to obtain

The magnitude equation is the familiar Ohm's law applied to the voltage and current amplitudes, while the second equation defines the phase relationship.
Validity of complex representation
This representation using complex exponentials may be justified by noting that (by Euler's formula):
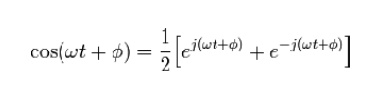
i.e. a real-valued sinusoidal function (which may represent our voltage or current waveform) may be broken into two complex-valued functions.
By the principle of superposition, we may analyze the behavior of the sinusoid on the left-hand side by analyzing the behavior of the two complex terms on the right-hand side. Given the symmetry, we only need to perform the analysis for one right-hand term; the results will be identical for the other. At the end of any calculation, we may return to real-valued sinusoids by further noting that
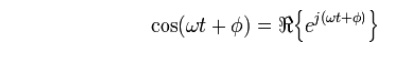
Phasors
A phasor is a constant complex number, usually expressed in exponential form, representing the complex amplitude (magnitude and phase) of a sinusoidal function of time. Phasors are used by electrical engineers to simplify computations involving sinusoids, where they can often reduce a differential equation problem to an algebraic one.
The impedance of a circuit element can be defined as the ratio of the phasor voltage across the element to the phasor current through the element, as determined by the relative amplitudes and phases of the voltage and current. This is identical to the definition from Ohm's law given above, recognizing that the factors of cancel.
Power quantities
When referring to measurements of power or intensity, a ratio can be expressed in decibels by evaluating ten times the base-10 logarithm of the ratio of the measured quantity to the reference level. Thus, if L represents the ratio of a power value P1 to another power value P0, then LdB represents that ratio expressed in decibels and is calculated using the formula:
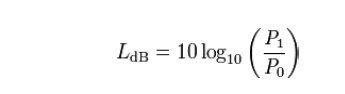
P1 and P0 must have the same dimension, i.e. they must measure the same type of quantity, and the same units before calculating the ratio: however, the choice of scale for this common unit is irrelevant, as it changes both quantities by the same factor, and thus cancels in the ratio—the ratio of two quantities is scale-invariant. Note that if P1 = P0 in the above equation, then LdB = 0. If P1 is greater than P0 then LdB is positive; if P1 is less than P0 then LdB is negative.
Rearranging the above equation gives the following formula for P1 in terms of P0 and LdB:
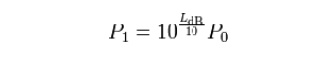
Since a bel is equal to ten decibels, the corresponding formulae for measurement in bels (LB) are
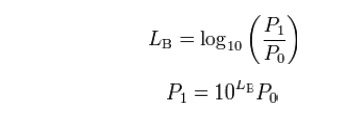
Related Topics