Test of Significance for Two Normal Population Variances

TEST OF SIGNIFICANCE FOR TWO NORMAL POPULATION VARIANCES

Test procedure:

This test compares the variances of two independent normal populations, viz., N(μ_X, σ_X²)

and N(μ_Y, σ_Y²).

Step 1 : Null Hypothesis H₀ : σ_X² = σ_Y²

That is, there is no significant difference between the variances of the two normal populations.

The alternative hypothesis can be chosen suitably from any one of the following

(i) H₁ : σ_X² < σ_Y² (ii) H₁ : σ_X² > σ_Y² (iii) H₁ : σ_X² ≠ σ_Y² 

Step 2 : Data

Let X₁, X₂,. . ., X_m and Y₁, Y₂,. . ., Y_n be two independent samples drawn from two normal populations respectively.

Step 3 : Level of significance

α

Step 4 : The test Statistic

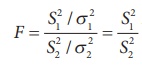 under H₀ and its sampling distribution under H₀ is F_{(m-1, n-1)}.

Step 5 : Calculation of the Test Statistic

The test statistic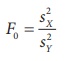 

Step 6 : Critical values

Step 7 : Decision

Note 1: Since f(m–1, n–1),1-α  is not avilable in the given F-table, it is computed as the reciprocal of f_{(n–1, m–1),α.}

Note 2: A F-test is based on the ratio of variances, it is also known as Variance Ratio Test.

Note 3: When μ_X and μ_Y are known, for testing the equality of variances of two normal populations, the test statistic is

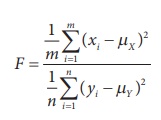 and follows F_{m, n}-distribution under H₀

Example 3.1

Two samples of sizes 9 and 8 give the sum of squares of deviations from their respective means as 160 inches square and 91 inches square respectively. Test the hypothesis that the variances of the two populations from which the samples are drawn are equal at 10% level of significance.

Solution:

Step 1 : Null Hypothesis: H₀ : σ_X² = σ_Y²

That is there is no significant difference between the two population variances.

Alternative Hypothesis: H₁ : σ_X² ≠ σ_Y²

That is there is significant difference between the two population variances.

Step 2 : Data

m = 9, n = 8

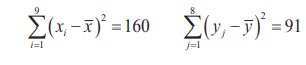
Step 3 : Level of significance

α = 10%

Step 4 : Test Statistic

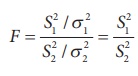 , under H₀.

Step 5 : Calculation

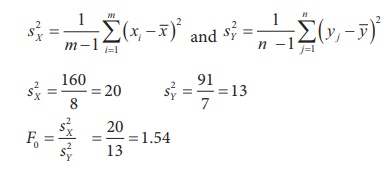
Step 6 : Critical values

Since H₁ is a two-sided alternative hypothesis the corresponding critical values are:

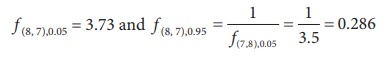
Step 7 : Decision

Since f _{(8, 7),0.95} = 0.286 < F₀ = 1.54 < f _{(8, 7),0.05} = 3.73, the null hypothesis is not rejected and we conclude that there is no significant difference between the two population variances.

Note 4: The critical values of F corresponding to α = 0.05 requires table values at 0.025 and 0.975 which are not provided. Hence α is taken as 0.1 in this example.

Example 3.2

A medical researcher claims that the variance of the heart rates (in beats per minute) of smokers is greater than the variance of heart rates of people who do not smoke. Samples from two groups are selected and the data is given below. Using = 0.05, test whether there is enough evidence to support the claim.

Solution:

Step 1 : Null Hypothesis: H₀ : σ₁² = σ₂²

That is there is no significant difference between the two population variances.

H₁ : σ₁² > σ₂²

That is, the variance of heart rates of smokers is greater than that of non-smokers.

Step 2 : Data

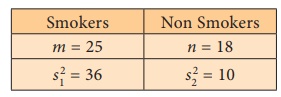
Step 3 : Level of significance α = 5%

Step 4 : Test statistic

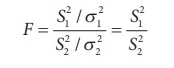
Step 5 : Calculation

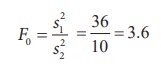
Step 6 : Critical value

f _{(m-1,n-1),0.05} = f _(24,17),0.05 = 2.19

Step 7 : Decision

Since F₀ = 3.6 > f _(24,17),0.05 = 2.19, the null hypothesis is rejected and we conclude that the variance of heart beats for smokers seems to be considerably higher compared to that of the non-smokers.

Example 3.3

The following table gives the random sample of marks scored by students in two schools, A and B.

Is the variance of the marks of students in school A is less than that of those in school B?

Test at 5% level of significance.

Solution:

Let X₁, X₂ , …, X_m represent sample values for school A and let Y₁, Y₂, …, Y_n represent sample values for school B.

Step 1 : Null Hypothesis: H₁ : σ_X² = σ_Y²

That is, there is no significant difference between the two population variances.

Alternative Hypothesis: H₁ : σ_X² < σ_Y²

That is, the variance of marks in school A is significantly less than that of school B.

Step 2 : Data

X₁, X₂,…, X_m are sample from school A

Y₁, Y₂, ..., Y_n are sample from school B

Step 3 : Test statistic

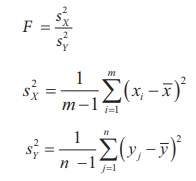
Step 4 : Calculations

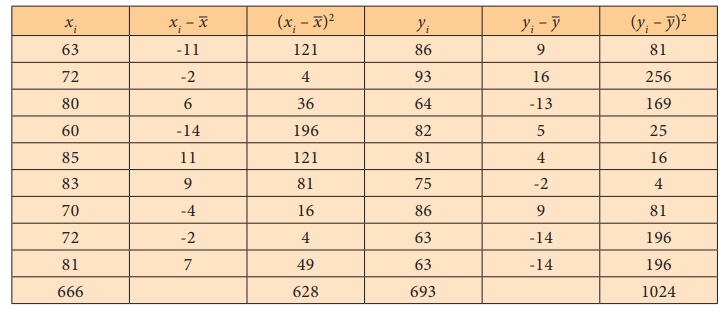
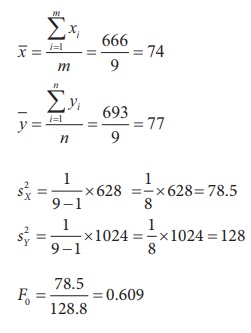
Step 5 : Level of significance

= 5%

Step 6 : Critical value

f_{(9-1,9-1),0.95} = 1/ f_{( 8 ,8),0.05} = 1/3.44  = 0.291

Step 7 : Decision

Since F ₀ = 0.609 > f_(8,8),0.95 = 0.291, the null hypothesis is not rejected and we conclude that in school B there seems to be more variance present than in school A.