Properties, Definition | Statistics - F -Distribution and Its Applications | 12th Statistics : Chapter 3 : Tests Based on Sampling Distributions II
Chapter: 12th Statistics : Chapter 3 : Tests Based on Sampling Distributions II
F -Distribution and Its Applications
F -DISTRIBUTION AND ITS APPLICATIONS
F-statistic is the ratio of two sums of the squares of deviations
of observations from respective means. The sampling distribution of the
statistic is F-distribution.
Definition: F -Distribution
Let X and Y be two independent χ2 random
variates with m and n degrees of freedom respectively.
Then F =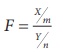 
is said to follow F-distribution with (m, n) degrees of freedom. This
F-distribution is named after the famous statistician R.A. Fisher (1890 to
1962).
Definition: F-Statistic
Let (X1, X2 , …, Xm)
and (Y1, Y2, …, Yn) be
two independent random samples drawn from N(μX, σX2)
and N(μY, σY2)
populations respectively.
Then,
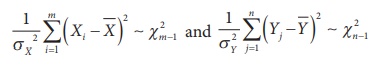
are
independent
(1)
Hence, F-Statistic is defined as
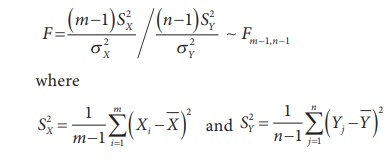
(2)
F-Statistic is also defined as the ratio of two mean square errors.
Applications of F-distribution
The following are some of the important applications where the
sampling distribution of the respective statistic under H0 is
F–distribution.
(i) Testing the equality of variances of two
normal populations. [Using (1)]
(ii) Testing the equality of means of k
(>2) normal populations. [Using (2)]
(iii) Carrying out analysis of variance for two-way classified
data. [Using (2)]
Related Topics