Tactics for Analysis

Tactics for Analysis

There are two clear plans of attack: a) determine the vector field for displace-ments and then differentiate to find the strains and stresses, or b) determine the tensor field and integrate to find the displacements. In either case, we can try all sorts of educated guesses or other tricks to shorten the process which, with either approach, is sometimes then called the semi-inverse method.

Direct Determination of Displacements

Direct determination of displacements is clearly the more obvious strategy and intuitively satisfying since this is what we actually see and can measure. Using the definitions of strains in terms of the relative displacements, and substituting the strain relationships Equation (3.2) becomes:

These are the Navier Field Equations* and they are very nice indeed. Fifteen equations have been reduced to only three second-order differential equations in terms of the components of the displacement vector field, which must be smooth and continuous. Moreover, if there is no volume change (naturally, or if = 0.5) and no body force, the displacement field is harmonic. Even if  is lin-ear and the body forces constant, the equations are manageable. Unfortunately, the complications introduced through the boundary conditions expressed in terms of displacements more than counterbalance the simplicity of the field equations and usually make the direct closed-form determination of the displacement field intractable.

Transforming the traction BCs [Equation (2.11)] and using the stress-strain

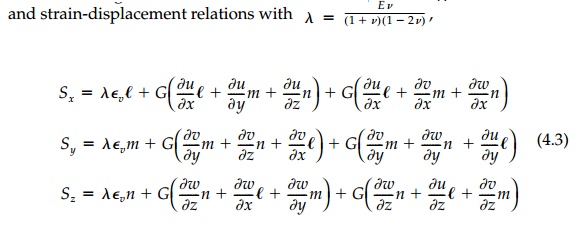
Seldom are the displacements or their derivatives known on the boundary and Equations (4.3) end up as integral equations which can only be evaluated numerically (the basis of the boundary integral method).

Direct Determination of Stresses

Direct determination of stresses is an alternative tactic for analysis. Finding a tensor field involving six unknowns rather than three would appear to be a step backwards, but it is not. Shortly after introducing the concept of stress in its general tensor representation, Cauchy* recognized its field properties and the advantages of expressing boundary conditions in terms of equilibrium. Combining the stress-strain relations with the compatibility Equation (3.6) and the equilibrium Equation (3.43), and letting:

In this case, _v is harmonic if the body force is constant or zero. Even some of the individual stress components can be harmonic in certain circumstances.

In summary, then,* we have developed two fundamental and unified descriptions of the intertwined scalar (_v and _v), vector (   Bar =  ui + vj + wk), and tensor ( _ij ? _ij ) fields of elasticity. We can try to either:

1.  Determine the vector displacement field and differentiate to obtain the tensor field, or

2.  Determine the tensor stress field, convert to strains and integrate, if possible, to obtain the vector field.

The first tactic is preferable in every way except in practice. We therefore will concentrate on the second approach for closed-form solutions although reference will often be made to the first, particularly in the chapter on torsion.