Integral Calculus - I - Summary | 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Chapter: 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Summary
Summary
In this chapter, we have acquired the
knowledge of
·
The
relation between the Primitive function and the derived function:
A function F (x) is said to be a
primitive function of the derived function f (x) , if d/dx [ F (x)]=
f (x)
·
Integration
of a function:
The process of determining an integral
of a given function is defined as integration of a function
·
Properties
of indefinite integrals:
∫af (x)
dx = a ∫ f (x) dx
∫ [f
(x) ± g (x) dx = ∫ f (x) dx ± ∫ g (x)
dx
·
Standard
results of indefinite integrals:
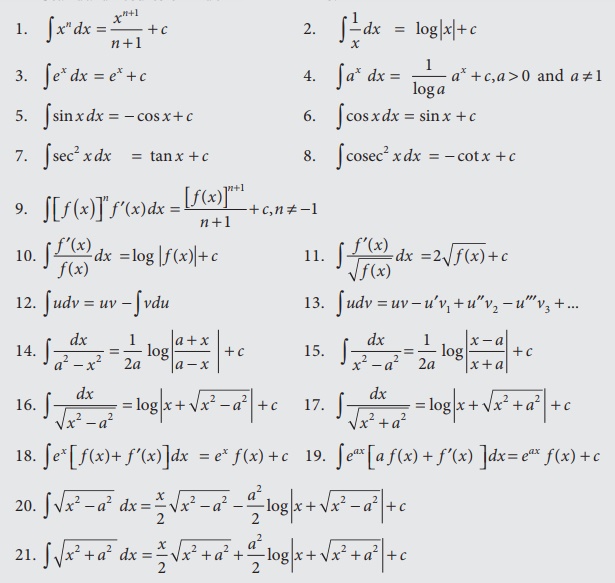
·
Definite
integral:
Let f ( x) be a continuous function on
[a,b] and if F(x) is anti derivative of f (x) , then
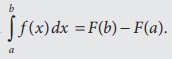
·
Properties
of definite integrals:
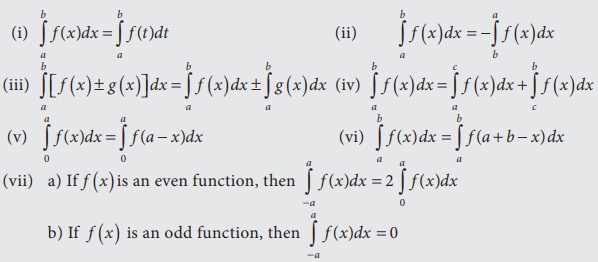
·
Particular
case of Gamma Integral:
If n is a positive integer, then 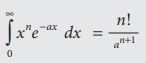
·
Properties
of gamma function:
(i) ┌(n) = (n-1) ┌ (n-1) , n > 1
(ii) ┌(n+1) = n┌ (n) , n > 0
(iii)
┌ (n + 1) = n!, n is a positive integer
(iv) ┌ ( 1/2 ) = √π
·
Definite
integral as the limit of a sum:
Let f (x) be a continuous real valued
function in [a , b], which is divided into n equal parts each of width h , then
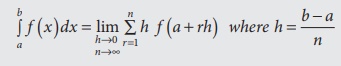
·
Results:
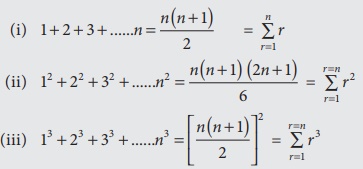
Related Topics