Exercise and Example Solved Problems with Answer, Solution | Methods of integration - Integration by parts Method | 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Chapter: 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Integration by parts Method
Integration by parts
Type: V
(1) We know that, if u and v are two differentiable functions of x ,
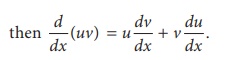
Integrate on both sides with respect to x .

This method is very useful when the integrand is a product of two different types of functions or a function which is not directly integrable. The success of this method depends on the proper choice of u . So we can choose the function u by using the following guidelines.
(i) If the integrand contains only a function which is directly not integrable, then take this as u.
(ii) If the integrand contains both directly integrable and non integrable functions, then take non integrable function as u.
(iii) If the integrand contains both the functions are integrable and one of them is of the form x n ,n is a positive integer, then take this xn as u.
(iv) for all other cases, the choice of u is ours.
(Or) we can also choose u as the function which comes first in the word “I L A T E” Where,
I stands for the inverse trigonometric function
L stands for the logarithmic function
A stands for the algebraic function
T stands for the trigonometric function
E stands for the exponential function and
take the remaining part of the function and dx as dv.
(2) If u and v are functions of x , then ∫udv = uv − u′v1 + u′′v 2 − u′′′v3 + ...
where u ′ , u′′, u′′′, . . . are the successive derivatives of u and v1 , v2 , v3 , . . . are the repeated integrals of v.
Note
The above mentioned formula is well known as Bernoulli’s formula.
Bernoulli’s formula is applied when u = xn where n is a positive integer.
Example



Exercise 2.5
Integrate the following with respect to x.
1. xe−x
2. x3 e3x
3. log x
4. x log x
5. xn log x
6. x5ex2
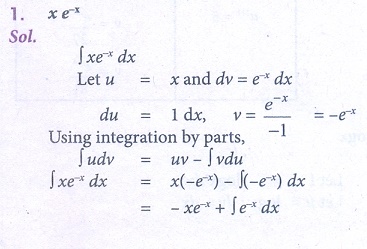

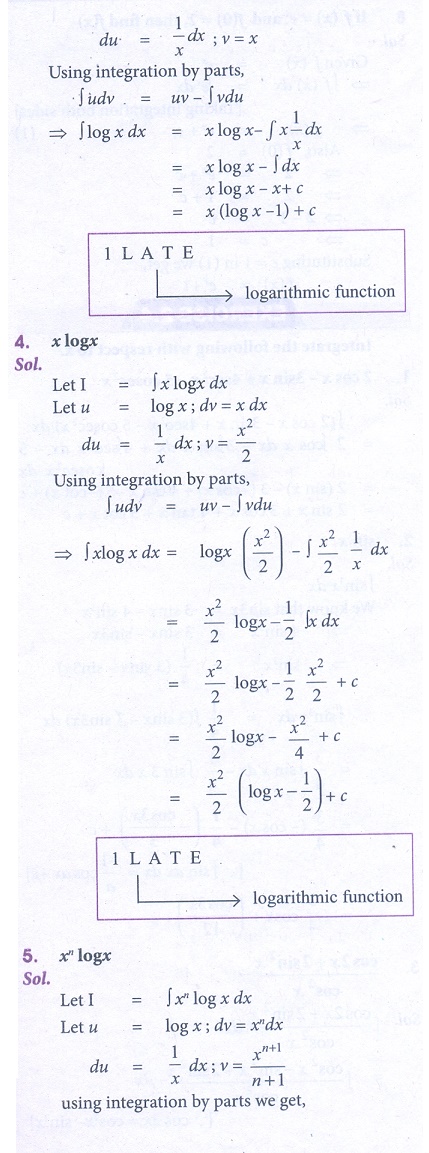


Answer:
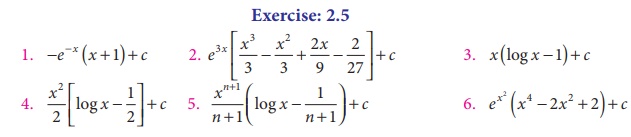
Related Topics