Concept of Indefinite Integral

Indefinite Integrals

Concept of Indefinite Integral

In differential calculus, we have learned how to calculate the differential coefficient f ′ (x) of a given function f (x) with respect to x. In this chapter, we have to find out the primitive function f (x) (i.e. original function) whenever its derived function f ′ (x) (i.e. derivative of a function) is given, such process is called integration or anti differentiation.

∴ Integration is the reverse process of differentiation

We know that d/dx (sin x ) = cos x. Here cos x is known as Derived function, and sin x is known as Primitive function [also called as Anti derivative function (or) Integral function].

Definition 2.1

A function F (x) is said to be a primitive function of the derived function f (x) , if d/dx [ F (x)]= f (x)

Now, consider the following examples which are already known to us.

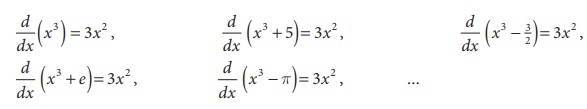
From the above examples, we observe that 3x² is the derived function of the primitive functions x³ , x³ + 5 , x³ – 3/2 , x ³ + e , x³ − π , ... and which indicates that the primitive functions are need not be unique, even though the derived function is unique. So we come to a conclusion that x ³ + c is the primitive function of the derived function 3x² .

∴ For every derived function, there are infinitely many primitives by choosing c arbitrarily from the set of real numbers R. So we called these integrals as indefinite integrals.

Definition 2.2

The process of determining an integral of a given function is defined as integration of a function.