Exercise and Example Solved Problems with Answer, Solution - Gamma Integral | 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Chapter: 12th Business Maths and Statistics : Chapter 2 : Integral Calculus - I
Gamma Integral
Gamma Integral
Gamma integral is an important result which is very useful in the evaluation of a particular type of an improper definite integrals.
First, let us know about the concepts of indefinite integrals, proper definite integrals and improper definite integrals
Indefinite integral:
An integral function which is expressed without limits, and so containing an arbitrary constant is called an indefinite integral
Example: ∫ e −tdt
Proper definite integral:
Proper definite integral is an integral function, which has both the limits a and b are finite and the integrand f(x) is continuous in [a, b].
Example: 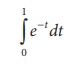
Improper definite integral:
An improper definite integral is an integral function, in which the limits either a or b or both are infinite, or the integrand f(x) becomes infinite at some points of the interval [a, b].
Example: ∞∫0e −tdt
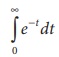

Properties:
1.┌ (n) = (n − 1)G(n − 1), n > 1
2.┌ (n + 1) = n┌ (n ), n > 0
3.┌(n + 1) = n! , n is a positive integer.
4.┌ (1/2 ) = p
Example 2.80

Exercise 2.10
1. Evaluate the following
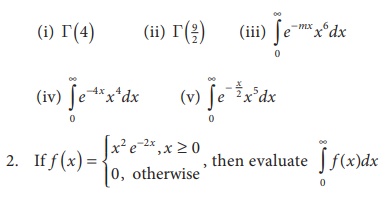

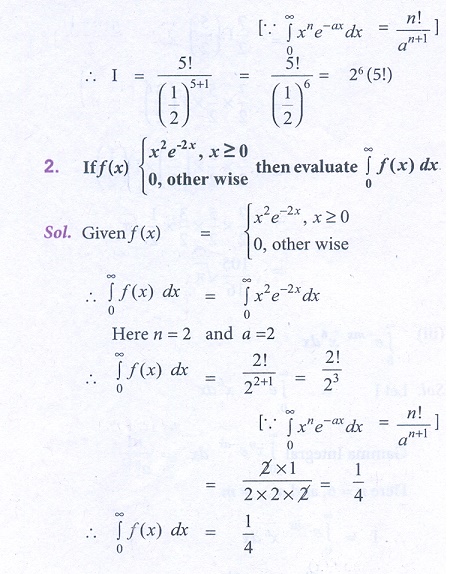
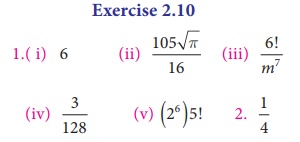
Related Topics