Chapter: Cryptography and Network Security Principles and Practice : One Symmetric Ciphers : Classical Encryption Techniques
Substitution Techniques
SUBSTITUTION TECHNIQUES
In this section and the next, we examine a sampling of what might be called classical encryption techniques. A study of these techniques enables us to illustrate the basic approaches to symmetric encryption used today and the types of cryptanalytic attacks that must be anticipated.
The two basic building blocks of all encryption techniques are substitution and transposition. We examine these in the next two sections. Finally, we discuss a system that combines both substitution and transposition.
A substitution technique is one in which the letters of plaintext are replaced by other letters or by numbers or symbols.1 If the plaintext is viewed as a sequence of bits, then substitution involves replacing plaintext bit patterns with ciphertext bit patterns.
Caesar Cipher
The earliest known, and the simplest, use of a substitution cipher was by Julius
Caesar. The Caesar cipher involves replacing each letter of the alphabet with the let-ter standing three places further down the alphabet. For example,
plain: meet me after the toga party
cipher: PHHW PH DIWHU WKH WRJD SDUWB
Note that the alphabet is wrapped around, so that the letter following Z is A. We can define the transformation by listing all possibilities, as follows:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
Let us assign a numerical equivalent to each letter:
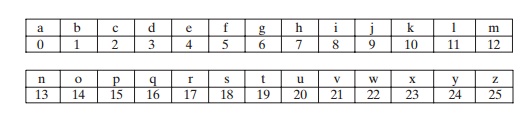
Then the algorithm can be expressed as follows. For each plaintext letter p, substi-tute the ciphertext letter C:2
C = E(3, p) = (p + 3) mod 26
A shift may be of any amount, so that the general Caesar algorithm is
C = E(k, p) = (p + k) mod 26 | (2.1) |
where k takes on a value in the range 1 to 25. The decryption algorithm is simply
p = D(k, C) = (C - k) mod 26 (2.2)
If it is known that a given ciphertext is a Caesar cipher, then a brute-force cryptanalysis is easily performed: simply try all the 25 possible keys. Figure 2.3 shows the results of applying this strategy to the example ciphertext. In this case, the plaintext leaps out as occupying the third line.
Three important characteristics of this problem enabled us to use a brute-force cryptanalysis:
1. The encryption and decryption algorithms are known.
2. There are only 25 keys to try.
3. The language of the plaintext is known and easily recognizable.
In most networking situations, we can assume that the algorithms are known. What generally makes brute-force cryptanalysis impractical is the use of an algo-
rithm that employs a large number of keys. For example, the triple DES algorithm, examined in Chapter 6, makes use of a 168-bit key, giving a key space of 2168 or greater than 3.7 * 1050 possible keys.


The third characteristic is also significant. If the language of the plaintext is unknown, then plaintext output may not be recognizable. Furthermore, the input may be abbreviated or compressed in some fashion, again making recogni-tion difficult. For example, Figure 2.4 shows a portion of a text file compressed using an algorithm called ZIP. If this file is then encrypted with a simple substi-tution cipher (expanded to include more than just 26 alphabetic characters), then the plaintext may not be recognized when it is uncovered in the brute-force cryptanalysis.
Monoalphabetic Ciphers
With only 25 possible keys, the Caesar cipher is far from secure. A dramatic increase in the key space can be achieved by allowing an arbitrary substitution. Before pro-ceeding, we define the term permutation. A permutation of a finite set of elements S is an ordered sequence of all the elements of S, with each element appearing exactly once. For example, if S = {a, b, c}, there are six permutations of S:
abc, acb, bac, bca, cab, cba
In general, there are n! permutations of a set of n elements, because the first element can be chosen in one of n ways, the second in n - 1 ways, the third in n - 2 ways, and so on.
Recall the assignment for the Caesar cipher:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
If, instead, the “cipher” line can be any permutation of the 26 alphabetic characters, then there are 26! or greater than 4 * 1026 possible keys. This is 10 orders of magni-tude greater than the key space for DES and would seem to eliminate brute-force techniques for cryptanalysis. Such an approach is referred to as a monoalphabetic substitution cipher, because a single cipher alphabet (mapping from plain alphabet to cipher alphabet) is used per message.
There is, however, another line of attack. If the cryptanalyst knows the nature of the plaintext (e.g., noncompressed English text), then the analyst can exploit the regularities of the language. To see how such a cryptanalysis might proceed, we give a partial example here that is adapted from one in [SINK66]. The ciphertext to be solved is
UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZ
VUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX
EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ
As a first step, the relative frequency of the letters can be determined and compared to a standard frequency distribution for English, such as is shown in Figure 2.5 (based on [LEWA00]). If the message were long enough, this technique alone might be sufficient, but because this is a relatively short message, we cannot expect an exact match. In any case, the relative frequencies of the letters in the ciphertext (in percentages) are as follows:
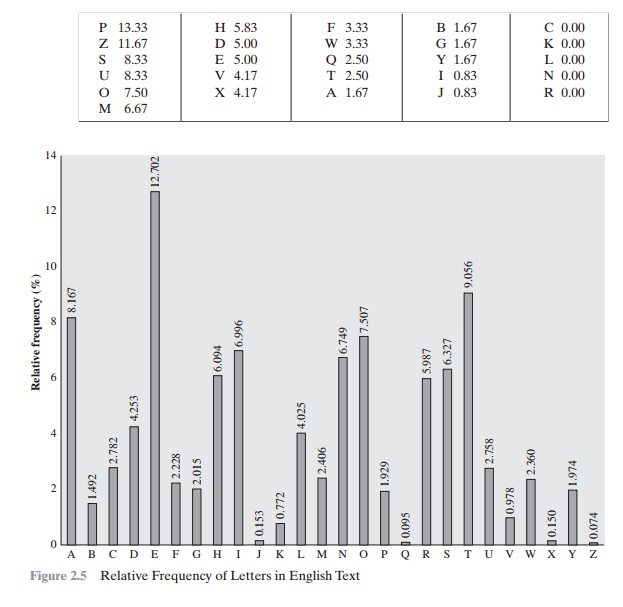
Comparing this breakdown with Figure 2.5, it seems likely that cipher letters P and Z are the equivalents of plain letters e and t, but it is not certain which is which. The letters S, U, O, M, and H are all of relatively high frequency and probably correspond to plain letters from the set {a, h, i, n, o, r, s}. The letters with the lowest frequencies (namely, A, B, G, Y, I, J) are likely included in the set {b, j, k, q, v, x, z}.
There are a number of ways to proceed at this point. We could make some tentative assignments and start to fill in the plaintext to see if it looks like a reasonable “skeleton” of a message. A more systematic approach is to look for other regularities. For example, certain words may be known to be in the text. Or we could look for repeating sequences of cipher letters and try to deduce their plaintext equivalents.
A powerful tool is to look at the frequency of two-letter combinations, known as digrams. A table similar to Figure 2.5 could be drawn up showing the relative fre-quency of digrams. The most common such digram is th. In our ciphertext, the most common digram is ZW, which appears three times. So we make the correspondence of Z with t and W with h. Then, by our earlier hypothesis, we can equate P with e. Now notice that the sequence ZWP appears in the ciphertext, and we can translate that sequence as “the.” This is the most frequent trigram (three-letter combination) in English, which seems to indicate that we are on the right track.
Next, notice the sequence ZWSZ in the first line. We do not know that these four letters form a complete word, but if they do, it is of the form th_t. If so, S equates with a.
So far, then, we have

Only four letters have been identified, but already we have quite a bit of the message. Continued analysis of frequencies plus trial and error should easily yield a solution from this point. The complete plaintext, with spaces added between words, follows:
it was disclosed yesterday that several informal but direct contacts have been made with political representatives of the viet cong in Moscow
Monoalphabetic ciphers are easy to break because they reflect the frequency data of the original alphabet. A countermeasure is to provide multiple substitutes, known as homophones, for a single letter. For example, the letter e could be assigned a number of different cipher symbols, such as 16, 74, 35, and 21, with each homophone assigned to a letter in rotation or randomly. If the number of symbols assigned to each letter is proportional to the relative frequency of that letter, then single-letter frequency information is completely obliterated. The great mathematician Carl Friedrich Gauss believed that he had devised an unbreakable cipher using homo-phones. However, even with homophones, each element of plaintext affects only one element of ciphertext, and multiple-letter patterns (e.g., digram frequencies) still survive in the ciphertext, making cryptanalysis relatively straightforward.
Two principal methods are used in substitution ciphers to lessen the extent to which the structure of the plaintext survives in the ciphertext: One approach is to encrypt multiple letters of plaintext, and the other is to use multiple cipher alphabets. We briefly examine each.
Playfair Cipher
The best-known multiple-letter encryption cipher is the Playfair, which treats digrams in the plaintext as single units and translates these units into ciphertext digrams.3
The Playfair algorithm is based on the use of a 5 x 5 matrix of letters con-structed using a keyword. Here is an example, solved by Lord Peter Wimsey in Dorothy Sayers’s Have His Carcase:
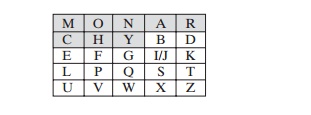
In this case, the keyword is monarchy. The matrix is constructed by filling in the letters of the keyword (minus duplicates) from left to right and from top to bot-tom, and then filling in the remainder of the matrix with the remaining letters in alphabetic order. The letters I and J count as one letter. Plaintext is encrypted two letters at a time, according to the following rules:
1. Repeating plaintext letters that are in the same pair are separated with a filler letter, such as x, so that balloon would be treated as ba lx lo on.
2. Two plaintext letters that fall in the same row of the matrix are each replaced by the letter to the right, with the first element of the row circularly following the last. For example, ar is encrypted as RM.
3. Two plaintext letters that fall in the same column are each replaced by the letter beneath, with the top element of the column circularly following the last. For example, mu is encrypted as CM.
4. Otherwise, each plaintext letter in a pair is replaced by the letter that lies in its own row and the column occupied by the other plaintext letter. Thus, hs becomes BP and ea becomes IM (or JM, as the encipherer wishes).
The Playfair cipher is a great advance over simple monoalphabetic ciphers. For one thing, whereas there are only 26 letters, there are 26 x 26 = 676 digrams,
that identification of individual digrams is more difficult. Furthermore, the relative frequencies of individual letters exhibit a much greater range than that of digrams, making frequency analysis much more difficult. For these reasons, the Playfair cipher was for a long time considered unbreakable. It was used as the standard field system by the British Army in World War I and still enjoyed considerable use by the U.S. Army and other Allied forces during World War II.
Despite this level of confidence in its security, the Playfair cipher is relatively easy to break, because it still leaves much of the structure of the plaintext language intact. A few hundred letters of ciphertext are generally sufficient.
One way of revealing the effectiveness of the Playfair and other ciphers is shown in Figure 2.6, based on [SIMM93]. The line labeled plaintext plots the frequency distri-bution of the more than 70,000 alphabetic characters in the Encyclopaedia Britannica article on cryptology. This is also the frequency distribution of any monoalphabetic substitution cipher, because the frequency values for individual letters are the same, just with different letters substituted for the original letters. The plot was developed in the following way: The number of occurrences of each letter in the text was counted and divided by the number of occurrences of the letter e (the most frequently used letter). As a result, e has a relative frequency of 1, t of about 0.76, and so on. The points on the horizontal axis correspond to the letters in order of decreasing frequency.
Figure 2.6 also shows the frequency distribution that results when the text is encrypted using the Playfair cipher. To normalize the plot, the number of occurrences of each letter in the ciphertext was again divided by the number of occurrences of e
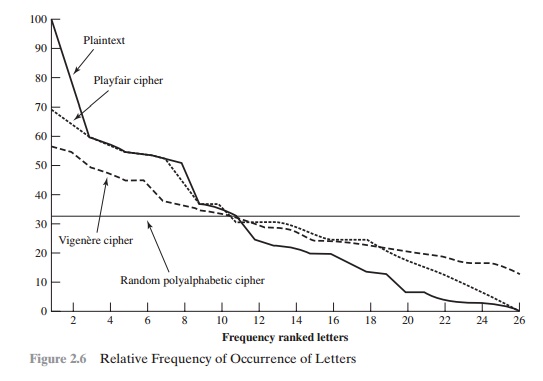
in the plaintext. The resulting plot therefore shows the extent to which the frequency distribution of letters, which makes it trivial to solve substitution ciphers, is masked by encryption. If the frequency distribution information were totally concealed in the encryption process, the ciphertext plot of frequencies would be flat, and cryptanalysis using ciphertext only would be effectively impossible. As the figure shows, the Playfair cipher has a flatter distribution than does plaintext, but nevertheless, it reveals plenty of structure for a cryptanalyst to work with.
Hill Cipher
Another interesting multiletter cipher is the Hill cipher, developed by the mathe-matician Lester Hill in 1929.
CONCEPTS FROM LINEAR ALGEBRA Before describing the Hill cipher, let us briefly review some terminology from linear algebra. In this discussion, we are concerned with matrix arithmetic modulo 26. For the reader who needs a refresher on matrix multiplication and inversion, see Appendix E.
We define the inverse M - 1 of a square matrix M by the equation M(M - 1) = M - 1M = I, where I is the identity matrix. I is a square matrix that is all zeros except for ones along the main diagonal from upper left to lower right. The inverse of a matrix does not always exist, but when it does, it satisfies the preceding equation. For example,
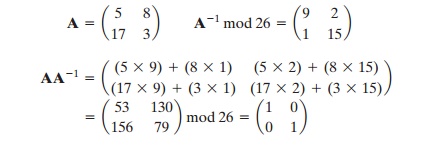
To explain how the inverse of a matrix is computed, we begin by with the con-cept of determinant. For any square matrix (m x m), the determinant equals the sum of all the products that can be formed by taking exactly one element from each row and exactly one element from each column, with certain of the product terms pre-ceded by a minus sign. For a 2 x 2 matrix,
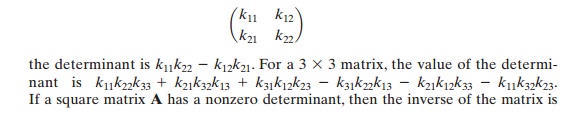

where C and P are row vectors of length 3 representing the plaintext and ciphertext, and K is a 3 * 3 matrix representing the encryption key. Operations are performed mod 26.
For example, consider the plaintext “paymoremoney” and use the encrypttion key
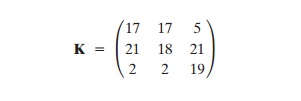
The first three letters of the plaintext are represented by the vector (15 0 24). Then (15 0 24)K = (303 303 531) mod 26 = (17 17 11) = RRL. Continuing in this fash-ion, the ciphertext for the entire plaintext is RRLMWBKASPDH.
Decryption requires using the inverse of the matrix K. We can compute det K = 23, and therefore, (det K)-1 mod 26 = 17. We can then compute the inverse as
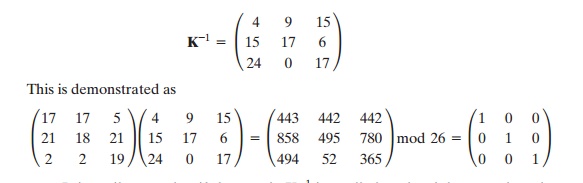
It is easily seen that if the matrix K - 1 is applied to the ciphertext, then the plaintext is recovered.
In general terms, the Hill system can be expressed as
C = E(K, P) = PK mod 26
P = D(K, C) = CK - 1 mod 26 = PKK - 1 = P
As with Playfair, the strength of the Hill cipher is that it completely hides single-letter frequencies. Indeed, with Hill, the use of a larger matrix hides more fre-quency information. Thus, a 3 * 3 Hill cipher hides not only single-letter but also two-letter frequency information.
Although the Hill cipher is strong against a ciphertext-only attack, it is easily broken with a known plaintext attack. For an m * m Hill cipher, suppose we have m plaintext–ciphertext pairs, each of length m. We label the pairs Pj = (p1j p1j ..... pmj) and Cj = (c1j c1j ..... cmj) such that Cj = PjK for 1 … j … m and for some unknown key matrix K. Now define two m * m matrices X = (pij) and Y = (cij) . Then we can form the matrix equation Y = XK. If X has an inverse, then we can determine K = X - 1Y. If X is not invertible, then a new version of X can be formed with additional plaintext–ciphertext pairs until an invertible X is obtained.
Consider this example. Suppose that the plaintext “hillcipher” is encrypted using a 2 * 2 Hill cipher to yield the ciphertext HCRZSSXNSP. Thus, we know that
(7 8)K mod 26 = (7 2); (11 11)K mod 26 = (17 25); and so on. Using the first two plaintext–ciphertext pairs, we have
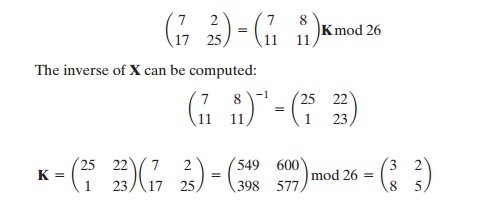
This result is verified by testing the remaining plaintext–ciphertext pairs.
Polyalphabetic Ciphers
Another way to improve on the simple monoalphabetic technique is to use different monoalphabetic substitutions as one proceeds through the plaintext message. The general name for this approach is polyalphabetic substitution cipher. All these tech-niques have the following features in common:
1. A set of related monoalphabetic substitution rules is used.
2. A key determines which particular rule is chosen for a given transformation.
VIGENERE` CIPHER The best known, and one of the simplest, polyalphabetic ciphers is the Vigenère cipher. In this scheme, the set of related monoalphabetic substitution rules consists of the 26 Caesar ciphers with shifts of 0 through 25. Each cipher is denoted by a key letter, which is the ciphertext letter that substitutes for the plaintext letter a. Thus, a Caesar cipher with a shift of 3 is denoted by the key value d.
We can express the Vigenère cipher in the following manner. Assume a sequence of plaintext letters P = p0, p1, p2, ..... , pn - 1 and a key consisting of the sequence of letters K = k0, k1, k2, ..... , km - 1, where typically m < n. The sequence of ciphertext letters C = C0, C1, C2, ..... , Cn - 1 is calculated as follows:
C = C0, C1, C2, ..... , Cn - 1 = E(K, P) = E[(k0, k1, k2, ..... , km - 1), (p0, p1, p2, ..... , pn - 1)]
= (p0 + k0) mod 26, (p1 + k1) mod 26, ..... , (pm - 1 + km - 1) mod 26,
(pm + k0) mod 26, (pm + 1 + k1) mod 26, ..... , (p2m - 1 + km - 1) mod 26, .....
Thus, the first letter of the key is added to the first letter of the plaintext, mod 26, the second letters are added, and so on through the first m letters of the plaintext. For the next m letters of the plaintext, the key letters are repeated. This process contin-ues until all of the plaintext sequence is encrypted. A general equation of the encryption process is
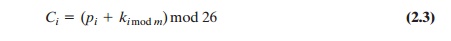
Compare this with Equation (2.1) for the Caesar cipher. In essence, each plaintext character is encrypted with a different Caesar cipher, depending on the corresponding key character. Similarly, decryption is a generalization of Equation (2.2):
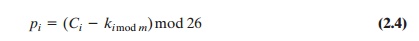
To encrypt a message, a key is needed that is as long as the message. Usually, the key is a repeating keyword. For example, if the keyword is deceptive, the message “we are discovered save yourself” is encrypted as
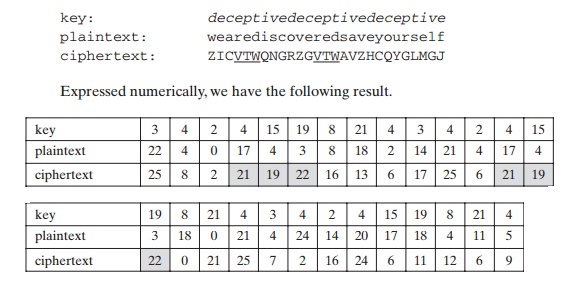
The strength of this cipher is that there are multiple ciphertext letters for each plaintext letter, one for each unique letter of the keyword. Thus, the letter frequency information is obscured. However, not all knowledge of the plaintext structure is lost. For example, Figure 2.6 shows the frequency distribution for a Vigenère cipher with a keyword of length 9. An improvement is achieved over the Playfair cipher, but considerable frequency information remains.
It is instructive to sketch a method of breaking this cipher, because the method reveals some of the mathematical principles that apply in cryptanalysis.
First, suppose that the opponent believes that the ciphertext was encrypted using either monoalphabetic substitution or a Vigenère cipher. A simple test can be made to make a determination. If a monoalphabetic substitution is used, then the statistical properties of the ciphertext should be the same as that of the language of the plaintext. Thus, referring to Figure 2.5, there should be one cipher letter with a relative frequency of occurrence of about 12.7%, one with about
9.06%, and so on. If only a single message is available for analysis, we would not expect an exact match of this small sample with the statistical profile of the plain-text language. Nevertheless, if the correspondence is close, we can assume a monoalphabetic substitution.
If, on the other hand, a Vigenère cipher is suspected, then progress depends on determining the length of the keyword, as will be seen in a moment. For now, let us con-centrate on how the keyword length can be determined.The important insight that leads to a solution is the following: If two identical sequences of plaintext letters occur at a dis-tance that is an integer multiple of the keyword length, they will generate identical ciphertext sequences. In the foregoing example, two instances of the sequence “red” are separated by nine character positions. Consequently, in both cases, r is encrypted using key letter e, e is encrypted using key letter p, and d is encrypted using key letter t. Thus, in both cases, the ciphertext sequence is VTW. We indicate this above by underlining the relevant ciphertext letters and shading the relevant ciphertext numbers.
An analyst looking at only the ciphertext would detect the repeated sequences VTW at a displacement of 9 and make the assumption that the keyword is either three or nine letters in length. The appearance of VTW twice could be by chance and not reflect identical plaintext letters encrypted with identical key letters. However, if the message is long enough, there will be a number of such repeated ciphertext sequences. By looking for common factors in the displacements of the various sequences, the analyst should be able to make a good guess of the keyword length.
Solution of the cipher now depends on an important insight. If the keyword length is m, then the cipher, in effect, consists of m monoalphabetic substitution ciphers. For example, with the keyword DECEPTIVE, the letters in positions 1, 10, 19, and so on are all encrypted with the same monoalphabetic cipher. Thus, we can use the known frequency characteristics of the plaintext language to attack each of the monoalphabetic ciphers separately.
The periodic nature of the keyword can be eliminated by using a nonrepeating keyword that is as long as the message itself. Vigenère proposed what is referred to as an autokey system, in which a keyword is concatenated with the plaintext itself to provide a running key. For our example,
key: deceptivewearediscoveredsav
plaintext: wearediscoveredsaveyourself
ciphertext: ZICVTWQNGKZEIIGASXSTSLVVWLA
Even this scheme is vulnerable to cryptanalysis. Because the key and the plain-text share the same frequency distribution of letters, a statistical technique can be applied. For example, e enciphered by e, by Figure 2.5, can be expected to occur with a frequency of (0.127)2 L 0.016, whereas t enciphered by t would occur only about half as often. These regularities can be exploited to achieve successful cryptanalysis.
VERNAM CIPHER The ultimate defense against such a cryptanalysis is to choose a keyword that is as long as the plaintext and has no statistical relationship to it. Such a system was introduced by an AT&T engineer named Gilbert Vernam in 1918. His system works on binary data (bits) rather than letters. The system can be expressed succinctly as follows (Figure 2.7):

where
pi = i th binary digit of plaintext ki = ith binary digit of key
ci = ith binary digit of ciphertext
Compare this with Equation (2.3) for the Vigenère cipher.
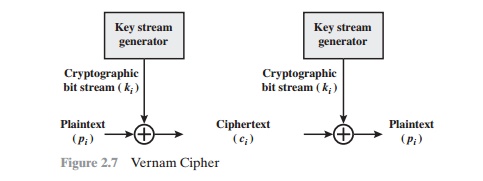
Thus, the ciphertext is generated by performing the bitwise XOR of the plain-text and the key. Because of the properties of the XOR, decryption simply involves the same bitwise operation:
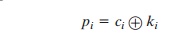
which compares with Equation (2.4).
The essence of this technique is the means of construction of the key. Vernam proposed the use of a running loop of tape that eventually repeated the key, so that in fact the system worked with a very long but repeating keyword. Although such a scheme, with a long key, presents formidable cryptanalytic diffi-culties, it can be broken with sufficient ciphertext, the use of known or probable plaintext sequences, or both.
One-Time Pad
An Army Signal Corp officer, Joseph Mauborgne, proposed an improvement to the Vernam cipher that yields the ultimate in security. Mauborgne suggested using a random key that is as long as the message, so that the key need not be repeated. In addition, the key is to be used to encrypt and decrypt a single message, and then is discarded. Each new message requires a new key of the same length as the new mes-sage. Such a scheme, known as a one-time pad, is unbreakable. It produces random output that bears no statistical relationship to the plaintext. Because the ciphertext contains no information whatsoever about the plaintext, there is simply no way to break the code.
An example should illustrate our point. Suppose that we are using a Vigenère scheme with 27 characters in which the twenty-seventh character is the space character, but with a one-time key that is as long as the message. Consider the ciphertext
ANKYODKYUREPFJBYOJDSPLREYIUNOFDOIUERFPLUYTS
We now show two different decryptions using two different keys:
ciphertext: ANKYODKYUREPFJBYOJDSPLREYIUNOFDOIUERFPLUYTS
key: pxlmvmsydofuyrvzwc tnlebnecvgdupahfzzlmnyih
plaintext: mr mustard with the candlestick in the hall
ciphertext: ANKYODKYUREPFJBYOJDSPLREYIUNOFDOIUERFPLUYTS
key: mfugpmiydgaxgoufhklllmhsqdqogtewbqfgyovuhwt
plaintext: miss scarlet with the knife in the library
Suppose that a cryptanalyst had managed to find these two keys. Two plausible plaintexts are produced. How is the cryptanalyst to decide which is the correct decryption (i.e., which is the correct key)? If the actual key were produced in a truly random fashion, then the cryptanalyst cannot say that one of these two keys is more likely than the other. Thus, there is no way to decide which key is correct and there-fore which plaintext is correct.
In fact, given any plaintext of equal length to the ciphertext, there is a key that produces that plaintext. Therefore, if you did an exhaustive search of all possible keys, you would end up with many legible plaintexts, with no way of knowing which was the intended plaintext. Therefore, the code is unbreakable.
The security of the one-time pad is entirely due to the randomness of the key. If the stream of characters that constitute the key is truly random, then the stream of characters that constitute the ciphertext will be truly random. Thus, there are no patterns or regularities that a cryptanalyst can use to attack the ciphertext.
In theory, we need look no further for a cipher. The one-time pad offers com-plete security but, in practice, has two fundamental difficulties:
1. There is the practical problem of making large quantities of random keys. Any heavily used system might require millions of random characters on a regular basis. Supplying truly random characters in this volume is a significant task.
2. Even more daunting is the problem of key distribution and protection. For every message to be sent, a key of equal length is needed by both sender and receiver. Thus, a mammoth key distribution problem exists.
Because of these difficulties, the one-time pad is of limited utility and is useful primarily for low-bandwidth channels requiring very high security.
The one-time pad is the only cryptosystem that exhibits what is referred to as perfect secrecy. This concept is explored in Appendix F.
Related Topics